RL Circuit Switching

Introduction

The RL switching / closing transient is one of the most common electrical transients that is encountered in practice, and is also the basis for the computation of short circuit currents.

Derivation

Figure 1. Basic RL switching circuit

Consider the basic switching circuit in the figure to the right, consisting of an AC voltage source V, a switch S, a resistance R and an inductance L (all ideal circuit elements). At time $t=0\,$, the switch S will close and complete the circuit. Suppose the voltage source can be characterised as a sinusoid (as a function of time):

$V(t)=V_{m}\sin(\omega t+\theta )\,$

Where $\theta \,$ is an arbitrary phase angle to capture the time of switching.

At the point of switching, the voltage is given by Kirchhoff's voltage law:

$V_{m}\sin(\omega t+\theta )=RI(t)+L{\frac {dI(t)}{dt}}\,$

The current $I(t)\,$ must reach a steady state current of:

$I_{s}={\frac {V}{Z}}={\frac {V}{R+j\omega L}}\,$ ... Equ. (1)

And have a steady state power factor:

$\cos {\phi _{s}}={\frac {R}{|Z|}}={\frac {R}{\sqrt {R^{2}+\omega ^{2}L^{2}}}}\,$

However, at $t=0\,$, $I(0)=0\,$ and the inductance $L\,$ will prevent the circuit from reaching the steady-state current instantaneously. Therefore, there must be some transient that will provide a continuous transition path from $I(0)=0\,$ to the steady-state current $I(t_{s})=I_{s}\,$.

Equation (1) can be re-written as follows:

$V_{m}\left[\sin(\omega t)\cos \theta +\cos(\omega t)\sin \theta \right]=RI(t)+L{\frac {dI(t)}{dt}}\,$

Taking the Laplace transform of both sides, we get:

$V_{m}\left({\frac {\omega \cos \theta }{s^{2}+\omega ^{2}}}+{\frac {s\sin \theta }{s^{2}+\omega ^{2}}}\right)=Ri(s)+sLi(s)-LI(0)\,$

We assume that the initial current $I(0)=0\,$, so therefore re-arranging the equation above we get:

$i(s)={\frac {V_{m}}{L}}\left({\frac {1}{{\frac {R}{L}}+s}}\right)\left({\frac {\omega \cos \theta }{s^{2}+\omega ^{2}}}+{\frac {s\sin \theta }{s^{2}+\omega ^{2}}}\right)\,$

$={\frac {V_{m}}{L}}\left[{\frac {\omega \cos \theta }{(s^{2}+\omega ^{2})({\frac {R}{L}}+s)}}+{\frac {s\sin \theta }{(s^{2}+\omega ^{2})({\frac {R}{L}}+s)}}\right]\,$ ... Equ. (2)

It can be shown that the expression ${\frac {1}{(s+\alpha )(s^{2}+\omega ^{2})}}$ can be simplified as follows:

${\frac {1}{(s+\alpha )(s^{2}+\omega ^{2})}}={\frac {1}{\alpha ^{2}+\omega ^{2}}}\left({\frac {1}{s+\alpha }}-{\frac {s}{s^{2}+\omega ^{2}}}+{\frac {\alpha }{s^{2}+\omega ^{2}}}\right)\,$

Therefore, the inverse Laplace transforms of the terms in Equation (2) can be evaluated in a fairly straightforward manner:

1st term: ${\mathcal {L}}^{-1}\left[{\frac {\omega \cos \theta }{(s^{2}+\omega ^{2})({\frac {R}{L}}+s)}}\right]={\frac {\omega \cos \theta }{\left({\frac {R}{L}}\right)^{2}+\omega ^{2}}}\left[e^{-{\frac {R}{L}}t}-\cos(\omega t)+{\frac {R}{\omega L}}\sin(\omega t)\right]\,$

2nd term: ${\mathcal {L}}^{-1}\left[{\frac {s\sin \theta }{(s^{2}+\omega ^{2})({\frac {R}{L}}+s)}}\right]={\frac {\sin \theta }{\left({\frac {R}{L}}\right)^{2}+\omega ^{2}}}\left[-{\frac {R}{L}}e^{-{\frac {R}{L}}t}+\omega \sin(\omega t)+{\frac {R}{L}}\cos(\omega t)\right]\,$

Combining the two terms together (and including the constants), we get the transient current:

$I(t)={\frac {V_{m}}{L\left({\frac {R}{L}}\right)^{2}+\omega ^{2}}}\left[(\omega \cos \theta -{\frac {R}{L}}\sin \theta )e^{-{\frac {R}{L}}t}+({\frac {R}{L}}\cos \theta +\omega \sin \theta )\sin(\omega t)-(\omega \cos \theta -{\frac {R}{L}}\sin \theta )\cos(\omega t)\right]\,$ ... Equ. (3)

Earlier, we found that the steady state power factor is:

$\cos {\phi _{s}}={\frac {R}{\sqrt {R^{2}+\omega ^{2}L^{2}}}}\,$

This can be re-arranged as follows:

$\cos {\phi _{s}}={\frac {R}{L}}{\frac {1}{\sqrt {({\frac {R}{L}})^{2}+\omega ^{2}}}}\,$

Likewise, the sine of the power angle is:

$\sin {\phi _{s}}={\frac {\omega }{\sqrt {({\frac {R}{L}})^{2}+\omega ^{2}}}}\,$

Using these two equations above, we can simplify Equation (3) even further:

$I(t)={\frac {V_{m}{\sqrt {({\frac {R}{L}})^{2}+\omega ^{2}}}}{L\left[\left({\frac {R}{L}}\right)^{2}+\omega ^{2}\right]}}\left[(\cos \theta \sin \phi _{s}-\sin \theta \cos \phi _{s})e^{-{\frac {R}{L}}t}+(\cos \theta \cos \phi _{s}+\sin \theta \sin \phi _{s})\sin(\omega t)-(\cos \theta \sin \phi _{s}-\sin \theta \cos \phi _{s})\cos(\omega t)\right]\,$

Using some angle sum and difference trigonometric identities, we get:

$I(t)={\frac {V_{m}}{\sqrt {(R^{2}+\omega ^{2}L^{2}}}}\left[(-\sin(\theta -\phi _{s})e^{-{\frac {R}{L}}t}+(\cos \theta \cos \phi _{s}+\sin(\theta -\phi _{s})\sin(\omega t)+(\cos(\theta -\phi _{s})\cos(\omega t)\right]\,$

Simplifying again with the same trig identities, we get the final equation:

$I(t)={\frac {V_{m}}{\sqrt {(R^{2}+\omega ^{2}L^{2}}}}\left[(\sin(\omega t+\theta -\phi _{s})-\sin(\theta -\phi _{s})e^{-{\frac {R}{L}}t}\right]\,$ ... Equ. (4)

Interpretation

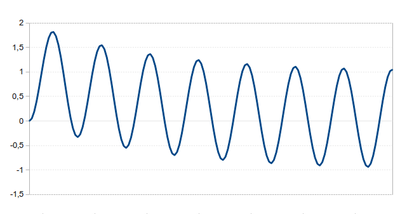
Figure 2. RL switching transient current

The figure right depicts a plot of the transient current in Equation (4) for the parameters R/L = 40 and switching angle $\theta$ = 0^o. Here we see the classic transient current waveform for an RL switching (closing) circuit with the time constant R/L.

Related Topics

• Short Circuit
• Transformer Inrush