Difference between revisions of "Overhead Line Constants"
(Created page with "left|thumb|700px|Figure 1. Circuit representation of a multi-conductor line segment <br clear=all> Image:DSCI0402.JPG|right|thumb|250px...") |
|||
| (One intermediate revision by the same user not shown) | |||
| Line 101: | Line 101: | ||
The Carson earth correction factors are infinite series (with terms that repeat in groups of four): | The Carson earth correction factors are infinite series (with terms that repeat in groups of four): | ||
| − | : <math>\Delta R_{ii}^{'} = 4\omega \times 10^{-4} \left( \frac{\pi}{8} - b_1 a \cos{\phi} + b_2 \left[ (c_2 - \ln{a}) a^2 \cos{2\phi} + \phi a^2 \sin{2\phi} \right] | + | : <math>\Delta R_{ii}^{'} = 4\omega \times 10^{-4} \left( \frac{\pi}{8} - b_1 a \cos{\phi} + b_2 \left[ (c_2 - \ln{a}) a^2 \cos{2\phi} + \phi a^2 \sin{2\phi} \right] + b_3 a^3 \cos{3\phi} - d_4 a^4 \cos{4\phi} - b_5 a^5 cos{5\phi} + b_6 \left[ (c_6 - \ln{a}) a^6 \cos{6\phi} + \phi a^6 \sin{6\phi} \right] + b_7 a^7 \cos{7\phi} - d_8 a^8 \cos{8\phi} + \dots \right) </math> |
| − | : <math>\Delta X_{ii}^{'} = 4\omega \times 10^{-4} \left( \frac{1}{2}(0.6159315 - \ln{a}) + b_1 a \cos{\phi} - d_2 a^2 \cos{2\phi} + b_3 a^3 \cos{3\phi} - b_4 \left[ (c_4 - \ln{a}) a^4 \cos{4\phi} + \phi a^4 \sin{4\phi} \right] | + | : <math>\Delta X_{ii}^{'} = 4\omega \times 10^{-4} \left( \frac{1}{2}(0.6159315 - \ln{a}) + b_1 a \cos{\phi} - d_2 a^2 \cos{2\phi} + b_3 a^3 \cos{3\phi} - b_4 \left[ (c_4 - \ln{a}) a^4 \cos{4\phi} + \phi a^4 \sin{4\phi} \right] + b_5 a^5 \cos{5\phi} - d_6 a^6 \cos{6\phi} + b_7 a^7 cos{7\phi} - b_8 \left[ (c_8 - \ln{a}) a^8 \cos{8\phi} + \phi a^8 \sin{8\phi} \right] + \dots \right) </math> |
where <math>a = 4\pi \sqrt{5} \times 10^{-4} \cdot D \sqrt{\frac{f}{\rho}} </math> | where <math>a = 4\pi \sqrt{5} \times 10^{-4} \cdot D \sqrt{\frac{f}{\rho}} </math> | ||
| Line 134: | Line 134: | ||
Assuming that the voltage in the earth conductors are zero (i.e. earth is the reference voltage), the earth conductors in the primitive series impedance and shunt admittance matrices can be eliminated by means of a [[Kron Reduction]]. | Assuming that the voltage in the earth conductors are zero (i.e. earth is the reference voltage), the earth conductors in the primitive series impedance and shunt admittance matrices can be eliminated by means of a [[Kron Reduction]]. | ||
| + | |||
| + | == Code == | ||
| + | |||
| + | Refer to this [https://github.com/susantoj/line-constants Github project] for an open-source Python implementation of a line constants calculation routine. | ||
[[Category:Modelling / Analysis]] | [[Category:Modelling / Analysis]] | ||
Latest revision as of 08:05, 22 November 2020

Consider the three-phase, single circuit tower line in Figure 2, which shows three phase conductors and an earth wire. A segmental length of this multi-conductor system can be represented by the equivalent circuit in Figure 1 above.
We can see that in a multi-conductor system, there is mutual coupling between the phase conductors (a, b and c), represented by the shunt inductances and capacitances. Note that there could also be resistive coupling between phases, but this is not shown in Figure 2 since resistive coupling is normally assumed to be negligible in overhead lines (i.e. shunt conductances G = 0).
This equivalent circuit can be represented as two Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n \times n} matrices (where n is the number of conductors in the system), one representing the series impedance Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [Z] \, } and the other representing the shunt admittance Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [Y] \, } .
For example, the four conductor system in Figure 2 has the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 4 \times 4 } series impedance matrix:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [Z] = \left[ \begin{matrix} Z_{aa} & Z_{ab} & Z_{ac} & | & Z_{ae}\\ Z_{ba} & Z_{bb} & Z_{bc} & | & Z_{be} \\ Z_{ca} & Z_{cb} & Z_{cc} & | & Z_{ce} \\ -- & -- & -- & | & -- \\ Z_{ea} & Z_{eb} & Z_{ec} & | & Z_{ee} \end{matrix} \right] \, }
And the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 4 \times 4 } shunt admittance matrix:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [Y] = \left[ \begin{matrix} Y_{aa} & Y_{ab} & Y_{ac} & | & Y_{ae}\\ Y_{ba} & Y_{bb} & Y_{bc} & | & Y_{be} \\ Y_{ca} & Y_{cb} & Y_{cc} & | & Y_{ce} \\ -- & -- & -- & | & -- \\ Y_{ea} & Y_{eb} & Y_{ec} & | & Y_{ee} \end{matrix} \right] \, }
Elements in the series impedance and shunt admittance matrices are complex quantities of the form: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_{ij} = R_{ij} + j X_{ij} \, } and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y_{ij} = G_{ij} + jB_{ij} \, } .
For most types of analyses, we can assume that the elements in the series impedance and shunt admittance matrices are constant terms without introducing too much error. These matrices are commonly called the overhead line constants and are calculated based on the overhead line conductor properties and cross-sectional geometry.
Assumptions
The following assumptions are made to simplify the line constants calculations:
- There is uniform current distribution in the conductor, thus conductor stranding is not taken into account
- The earth is flat along the length of the transmission line, i.e. earth curvature not allowed for
- Uniform soil conditions along the length of the transmission line, i.e. constant soil resistivity
Series Impedance Matrix
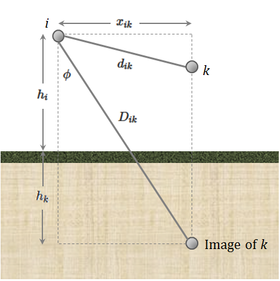
The lengths and angles referred to in the calculations below are all based on the geometry of two aerial conductors i and k shown in Figure 3.
Self Impedance Terms
The self impedance of an aerial conductor is calculated as follows:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_{ii}^{'} = \left( R_{int}^{'} + \Delta R_{ii}^{'} \right) + j \left( X_{int}^{'} + X_{geo}^{'} + \Delta X_{ii}^{'} \right) }
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{int}^{'}} is the internal resistance of the conductor (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega} /km)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_{int}^{'}} is the internal reactance of the conductor (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega} /km)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_{geo}^{'}} is the geometrical reactance (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega} /km)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta R_{ii}^{'}} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta X_{ii}^{'}} are the Carson earth correction factors (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega} /km) - see separate section below
When skin effect is not taken into account, the internal resistance is simply the DC resistance of the conductor Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{int}^{'} = R_{dc}} .
The internal reactance of the conductor depends on the type of conductor used, e.g. solid conductor (AAAC) vs a tubular conductor, where there is a non-conducting reinforcing material in the centre of the conductor (ACSR).
The reactance of a solid conductor (in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega} /km) is calculated as follows:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_{int}^{'} = 1000 \times j \omega \frac{\mu_0}{8\pi} }
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu_0} is the permeability of free space (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 4\pi \times 10^{-7 }} H/m)
The reactance of a tubular / hollow core conductor (in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega} /km) is calculated as follows:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_{int}^{'} = 1000 \times j \omega \frac{\mu_0}{2\pi} \left[ \frac{q^4}{(r^2-q^2)^2} \cdot \ln{\frac{r}{q}} \cdot \frac{3q^2-r^2}{4(r^2-q^2)} \right] }
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega} is the nominal angular frequency of the system (rad/s)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r} is the inner radius of the tubular conductor (m)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q} is the outer radius of the tubular conductor (m)
The geometrical reactance (in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega} /km) can be calculated as follows:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_{geo}^{'} = 1000 \times \omega \frac{\mu_0}{2\pi} \ln \left( \frac{2h_i}{r_i} \right)}
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_i} is the radius of the conductor (m)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h_i} is the height of the conductor above ground level (m)
Mutual Impedance Terms
The mutual impedance between any two aerial conductors is calculated as follows:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_{ik}^{'} = Z_{ki}^{'} = \Delta R_{ik}^{'} + j \left( X_{geo,i,k}^{'} + \Delta X_{ik}^{'} \right) }
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_{geo,i,k}^{'}} is the geometrical reactance between conductors i and k (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega} /km)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta R_{ik}^{'}} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta X_{ik}^{'}} are the Carson earth correction factors (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega} /km) - see separate section below
The geometrical reactance between conductors i and k (in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega} /km) can be calculated as follows:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_{geo,i,k}^{'} = 1000 \times \omega \frac{\mu_0}{2\pi} \ln \left( \frac{D_{ik}}{d_{ik}} \right) }
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_{ik}} is the distance between conductor i and conductor k (m)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D_{ik}} is the distance between conductor i and the image of conductor k in the ground (m)
Carson Earth Correction Factors
Because the earth/ground is a conducting medium, it has an effect on the magnetic field produced by the current flowing in an aerial conductor. During unbalanced operation or in single-phase earth return (SWER) systems, the earth also acts as a conductor for currents to return to the source.
The Carson earth correction factors are infinite series (with terms that repeat in groups of four):
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta R_{ii}^{'} = 4\omega \times 10^{-4} \left( \frac{\pi}{8} - b_1 a \cos{\phi} + b_2 \left[ (c_2 - \ln{a}) a^2 \cos{2\phi} + \phi a^2 \sin{2\phi} \right] + b_3 a^3 \cos{3\phi} - d_4 a^4 \cos{4\phi} - b_5 a^5 cos{5\phi} + b_6 \left[ (c_6 - \ln{a}) a^6 \cos{6\phi} + \phi a^6 \sin{6\phi} \right] + b_7 a^7 \cos{7\phi} - d_8 a^8 \cos{8\phi} + \dots \right) }
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta X_{ii}^{'} = 4\omega \times 10^{-4} \left( \frac{1}{2}(0.6159315 - \ln{a}) + b_1 a \cos{\phi} - d_2 a^2 \cos{2\phi} + b_3 a^3 \cos{3\phi} - b_4 \left[ (c_4 - \ln{a}) a^4 \cos{4\phi} + \phi a^4 \sin{4\phi} \right] + b_5 a^5 \cos{5\phi} - d_6 a^6 \cos{6\phi} + b_7 a^7 cos{7\phi} - b_8 \left[ (c_8 - \ln{a}) a^8 \cos{8\phi} + \phi a^8 \sin{8\phi} \right] + \dots \right) }
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a = 4\pi \sqrt{5} \times 10^{-4} \cdot D \sqrt{\frac{f}{\rho}} }
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b_i = b_{i-2} \cdot \frac{sign}{i(i+2)} } with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b_1 = \frac{\sqrt{2}}{6} } , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b_2 = \frac{1}{16} } and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle sign} alternating in groups of 4, i.e. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle sign = +1} for i=1,2,3,4, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle sign = -1} for i=5,6,7,8, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle sign = +1} for i=9,10,11,12 and so on
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_i = c_{i-2} + \frac{1}{i} + \frac{1}{i+2}} with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_2 = 1.3659315}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_i = \frac{\pi}{4} b_i }
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho } is the soil resistivity (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega \cdot m} )
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D = 2 h_i } for self impedance terms and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D = D_{ik} } for mutual impedance terms
Note that this formulation is only valid if Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a<5} .
Shunt Admittance Matrix
The self potential terms of the shunt admittance matrix are calculated as follows:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y_{ii}^{'} = 1000 \times \omega \frac{1}{2\pi \epsilon_0} \ln \left( \frac{2h_i}{r_i} \right) }
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_i} is the radius of the conductor (m)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h_i} is the height of the conductor above ground level (m)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_0} is the permittivity of free space (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 8.85418782 \times 10^{-12} } F/m)
The mutual potential terms of the shunt admittance matrix are calculated as follows:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y_{ik}^{'} = 1000 \times \omega \frac{1}{2\pi \epsilon_0} \ln \left( \frac{D_{ik}}{d_{ik}} \right) }
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_{ik}} is the distance between conductor i and conductor k (m)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D_{ik}} is the distance between conductor i and the image of conductor k in the ground (m)
Kron Reduction
Assuming that the voltage in the earth conductors are zero (i.e. earth is the reference voltage), the earth conductors in the primitive series impedance and shunt admittance matrices can be eliminated by means of a Kron Reduction.
Code
Refer to this Github project for an open-source Python implementation of a line constants calculation routine.