Difference between revisions of "Short Circuit"
(Created page with "A short circuit is an electrical fault where a conductive path (usually of low impedance) is formed between two or more conductive parts of an electrical system (e.g. phase-ph...") |
|||
| Line 51: | Line 51: | ||
In short circuits occurring far from synchronous generators, we can ignore the effects of the generator subtransient behaviour. It can be shown through [[RL_Circuit_Switching|transient circuit analysis]] that the maximum far-from-generator short circuit is as follows: | In short circuits occurring far from synchronous generators, we can ignore the effects of the generator subtransient behaviour. It can be shown through [[RL_Circuit_Switching|transient circuit analysis]] that the maximum far-from-generator short circuit is as follows: | ||
| − | : <math> i_{sc}(t) = \frac {E \sqrt{2}}{Z_{sc}} \left[ \sin \left( \omega t + \ | + | : <math> i_{sc}(t) = \frac {E \sqrt{2}}{Z_{sc}} \left[ \sin \left( \omega t + \phi \right) - \sin \phi e^{-\frac{R}{X} \omega t} \right] \, </math> |
Where <math>E \, </math> is the rms voltage of the circuit (V) | Where <math>E \, </math> is the rms voltage of the circuit (V) | ||
:: <math> Z_{sc} \, </math> is the fault impedance (<math>\Omega</math>) | :: <math> Z_{sc} \, </math> is the fault impedance (<math>\Omega</math>) | ||
:: <math> \frac{R}{X} \, </math> is the R/X ratio at the point of fault (pu) | :: <math> \frac{R}{X} \, </math> is the R/X ratio at the point of fault (pu) | ||
| + | :: <math> \phi </math> is a phase angle comprising the angle at the time of fault and the steady-state power angle (rad) | ||
We can see that there are two components: | We can see that there are two components: | ||
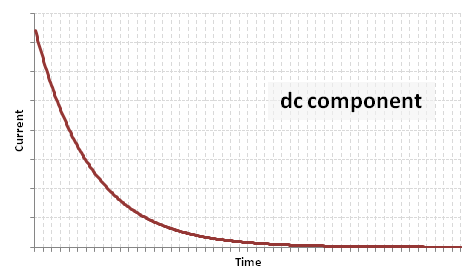
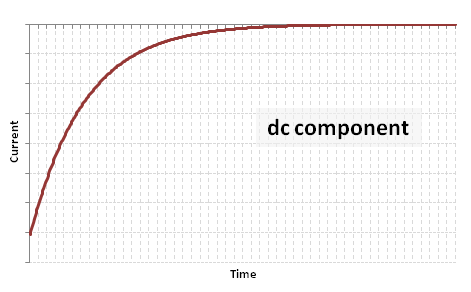
| − | (1) A decaying aperiodic component: <math> - \frac {E \sqrt{2}}{Z_{sc}} e^{-\frac{R}{X} \omega t} \, </math> | + | (1) A decaying aperiodic component: <math> - \frac {E \sqrt{2}}{Z_{sc}} \sin + \phi e^{-\frac{R}{X} \omega t } \, </math> |
[[Image:FFG_dc.PNG]] | [[Image:FFG_dc.PNG]] | ||
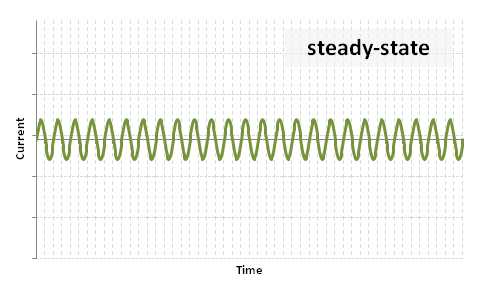
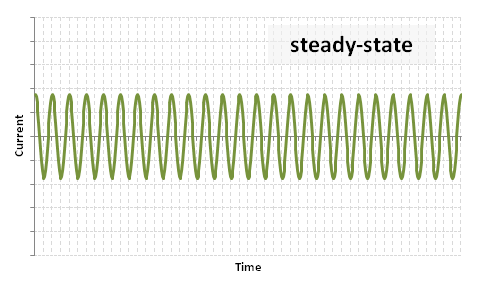
| − | (2) A steady state component: <math> \frac {E \sqrt{2}}{Z_{sc}} \sin \left( \omega t + \ | + | (2) A steady state component: <math> \frac {E \sqrt{2}}{Z_{sc}} \sin \left( \omega t + + \phi \right) \, </math> |
[[Image:FFG_steady.PNG]] | [[Image:FFG_steady.PNG]] | ||
Revision as of 13:47, 22 November 2020
A short circuit is an electrical fault where a conductive path (usually of low impedance) is formed between two or more conductive parts of an electrical system (e.g. phase-phase, phase-earth, phase-neutral, etc). This article looks at the nature of short circuits and tries to break down and explain the constituent parts of fault currents. Note that the terms "short circuit" and "fault" are often used interchangeably.
In most networks, a short circuit is similar to the closing transient of an RL circuit, where the R and L components are the impedances of the source(s). The transient characteristics of short circuit currents vary depending on whether they are near or far from synchronous generators. The sections below describe the two general types of short circuits:
Near-to-Generator Short Circuit
A fault close to a synchronous generator has the following maximum short circuit current Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i_{sc}(t)} :
Where is the phase-to-neutral rms voltage at the generator terminals (V)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_{d}'' \, } is the generator direct-axis subtransient reactance ()
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_{d}' \, } is the generator direct-axis transient reactance ()
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_{d} \, } is the generator synchronous reactance (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega} )
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{d}'' \, } is the generator subtransient time constant (s)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{d}' \, } is the generator transient time constant (s)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{a} \, } is the aperiodic time constant (s)
From the above equation, it can be seen that the short circuit current can be broken up into an aperiodic current (dc component of the short circuit):
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{E \sqrt{2}}{X_{d}''} e^{-t/t_{a}} \, }
And a series of three damped sinusoidal waveforms corresponding to the following distinct stages:
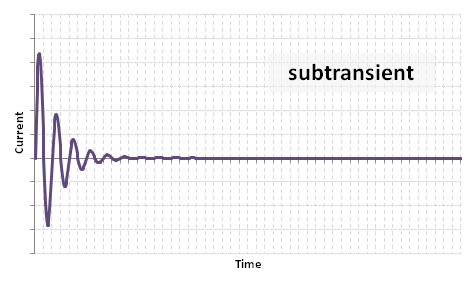
(1) Subtransient component: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E \sqrt{2} \left( \frac{1}{X_{d}''} - \frac{1}{X_{d}'} \right) e^{-t/t_{d}''} \sin (\omega t) \, }
This period typically lasts 10 to 20ms from the start of the fault. The subtransient reactance is due to the flux casued by the stator currents crossing the air gap and reaching the rotor surface or amortisseur / damper windings.
(2) Transient component: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E \sqrt{2} \left( \frac{1}{X_{d}'} - \frac{1}{X_{d}} \right) e^{-t/t_{d}'} \sin (\omega t) \, }
This period typically lasts 100 to 400ms after the subtransient period. The transient reactance occurs when all the damping currents in the rotor surface or amortisseur / damper windings have decayed, but while the damping currents in the field winding are still in action.
(3) Steady-state component: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E \sqrt{2} \frac{1}{X_{d}} \sin (\omega t) \, }
The steady-state occurs after the transient period when all the damping currents in the field windings have decayed, and essentially remains until the fault is cleared.
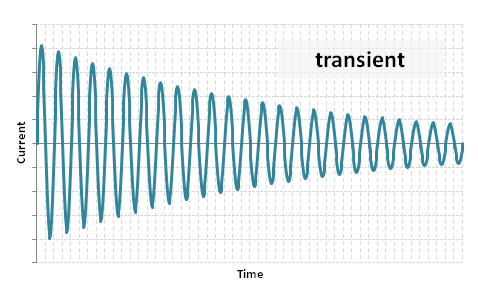
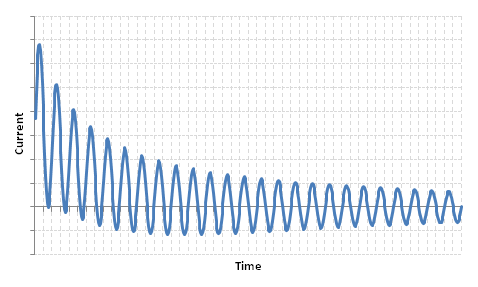
Putting these all together, we get the familiar near-to-generator short circuit waveform:
Far-from-Generator Short Circuit
In short circuits occurring far from synchronous generators, we can ignore the effects of the generator subtransient behaviour. It can be shown through transient circuit analysis that the maximum far-from-generator short circuit is as follows:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i_{sc}(t) = \frac {E \sqrt{2}}{Z_{sc}} \left[ \sin \left( \omega t + \phi \right) - \sin \phi e^{-\frac{R}{X} \omega t} \right] \, }
Where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E \, } is the rms voltage of the circuit (V)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_{sc} \, } is the fault impedance (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega} )
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{R}{X} \, } is the R/X ratio at the point of fault (pu)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi } is a phase angle comprising the angle at the time of fault and the steady-state power angle (rad)
We can see that there are two components:
(1) A decaying aperiodic component: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle - \frac {E \sqrt{2}}{Z_{sc}} \sin + \phi e^{-\frac{R}{X} \omega t } \, }
(2) A steady state component: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac {E \sqrt{2}}{Z_{sc}} \sin \left( \omega t + + \phi \right) \, }
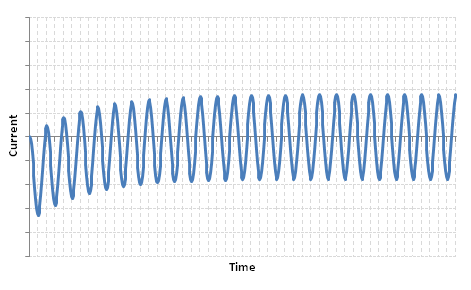
Putting these together, we get the total far-from-generator fault current:
During the transient period, the peak transient current is typically 1.5 to 2.5 times higher than the peak steady state current.
![{\displaystyle i_{sc}(t)=E{\sqrt {2}}\left[\left({\frac {1}{X_{d}''}}-{\frac {1}{X_{d}'}}\right)e^{-t/t_{d}''}+\left({\frac {1}{X_{d}'}}-{\frac {1}{X_{d}}}\right)e^{-t/t_{d}'}+{\frac {1}{X_{d}}}\right]\sin(\omega t)+{\frac {E{\sqrt {2}}}{X_{d}''}}e^{-t/t_{a}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8de4beceba71dfebc403b458538a020745f43839)