Simple Power Flow Example

From Open Electrical
Revision as of 14:04, 18 November 2020 by Jules (talk | contribs) (Created page with "Consider the simple model shown in Figure 1, where a large stiff network supplies a constant power load <math>\boldsymbol{S} \, </math> through an impedance <...")
(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)
Jump to navigation Jump to search

Consider the simple model shown in Figure 1, where a large stiff network supplies a constant power load Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{S} \, } through an impedance Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{Z_{s}}} :

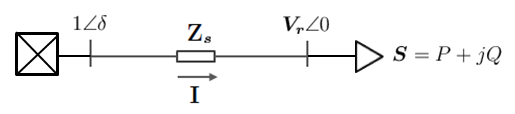
Figure 1. Simple power flow model (note that all quantities are in per-unit)


Suppose the load power Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{S} \, } is known and we want to calculate the load bus voltage Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{r} \, } . Unfortunately, this cannot be computed in a straightforward manner because the load is of constant power and thus the load current and impedance are voltage dependent, i.e. the load draws more current as voltage decreases. As a result, the load bus voltage is non-linearly related to the load itself.

Derivation of the Load Bus Voltage

Note that in this derivation, all quantities are in per-unit. Recall that the load complex power can be calculated from the voltage and current phasors as follows:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{S} = \boldsymbol{V_{r}} \boldsymbol{I}^{*} \, }
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = V_{r} \angle 0 \left( \frac{1 \angle \delta - V_{r} \angle 0}{\boldsymbol{Z_{s}}} \right)^{*} \, }

Suppose that we represent both the load power Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{S} \, } and impedance Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{Z_{s}}} in polar coordinates, i.e.

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{S} = S \angle \phi \, }
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{Z_{s}} = Z \angle \theta \, }

Then the power equation can be re-written as:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S \angle \phi = V_{r} \angle 0 \left( \frac{1 \angle \delta - V_{r} \angle 0}{Z \angle \theta} \right)^{*} \, }


Conjugating the terms in brackets and simplifying, we get:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S \angle \phi \times Z \angle (\theta) = V_{r} \angle (\delta) - V_{r}^{2} \, }
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle SZ \angle (\phi + \theta) + V_{r}^{2} = V_{r} \angle (\delta) \, }


Applying Euler's law, we get:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle SZ \left[ \cos(\phi + \theta) +j \sin(\phi -\theta) \right] + V_{r}^{2} = V_{r} \left[ \cos(\delta) + j \sin(\delta) \right] \, }

Separating the real and imaginary terms of the above equation:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle SZ \cos(\phi + \theta) + V_{r}^{2} = V_{r} \cos(\delta) \, }
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle SZ \sin(\phi + \theta) = V_{r} \sin(\delta) \, }

Squaring both equations and summing them together, we get:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[ SZ \cos(\phi + \theta) + V_{r}^{2} \right]^2 + (SZ)^{2} \sin^{2}(\phi + \theta) = V_{r}^{2} \cos^{2}(\delta) + V_{r}^{2} \sin^{2}(\delta) \, }

Simplifying and re-arranging the equation above, we can get the following homogenous equation:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{r}^{4} + \left[ 2SZ \cos(\phi + \theta) - 1 \right] V_{r}^{2} + (SZ)^{2} = 0 \, }

This equation can be solved for the load bus voltage Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{r} \, } using the quadratic formula:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{r} = \sqrt{\frac{-b \pm \sqrt{b^{2} - 4c}}{2}} \, } ... Equ. (1)

Where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b = 2SZ \cos(\phi + \theta) - 1 \, }

and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c = (SZ)^{2} \, }

Worked Example

Suppose that the source bus has a nominal voltage of 33kV and a short circuit level of 800MVA at X/R ratio of 10. What is the voltage at the load bus if it is supplying a constant 50MW load at 0.8pf (lagging)?

The source impedance is:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ||Z_{s}|| = \frac{V^{2}}{S_{SC}} = \frac{33kV^{2}}{800MVA} = 1.361 \Omega \, }

Converted to per-unit values (on a 100MVA base):

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ||Z_{s,pu}|| = \frac{||Z_{s}||}{Z_{base}} = \frac{1.361}{4.84} = 0.281 pu \, }

For an X/R ratio of 10, the source impedance is therefore:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{Z_{s,pu}} = 0.02799 + j0.2799 pu = 0.281 \angle 1.471 \, } (angle in radians)

The 50MW load converted to per unit is (by convention, a load with lagging power factor has a negative reactive power):

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{S_{pu}} = 0.5 - j0.375 pu = 0.625 \angle -0.6435 \, } (angle in radians)

Plugging the parameters Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S = 0.625 \, } , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z = 0.281 \, } , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi = -0.6435 \, } and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta = 1.471 \, } into Equation (1), we get the load bus voltage:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_r = 0.8480 pu \, }

Intuition for General Power Flow Solutions

We saw in this simple example that the power flow problem for constant power loads is non-linear (i.e. quadratic) and cannot be solved with linear techniques. This intuition can be extended to more general power flow problems. While a closed form solution was found for this simple case, the general power flow problem is typically solved using iterative numerical methods, for example a Newton-Raphson algorithm.

Retrieved from "http://openelectrical.org/index.php?title=Simple_Power_Flow_Example&oldid=40"