|
|
| Line 1: |
Line 1: |
| | == Introduction == | | == Introduction == |
| | | | |
| − | The RL switching / closing transient is one of the most common electrical transients that is encountered in practice, and is also the basis for the computation of [[Short_Circuit_Calculation|short circuit currents]]. | + | The RL switching / closing transient is one of the most common electrical transients that is encountered in practice, and is also the basis for the computation of [[Short Circuit|short circuit currents]]. |
| | | | |
| | == Derivation == | | == Derivation == |
| Line 88: |
Line 88: |
| | | | |
| | The figure right depicts a plot of the transient current in Equation (4) for the parameters R/L = 40 and switching angle <math>\theta</math> = 0<sup>o</sup>. Here we see the classic transient current waveform for an RL switching (closing) circuit with the time constant R/L. | | The figure right depicts a plot of the transient current in Equation (4) for the parameters R/L = 40 and switching angle <math>\theta</math> = 0<sup>o</sup>. Here we see the classic transient current waveform for an RL switching (closing) circuit with the time constant R/L. |
| | + | |
| | + | == Related Topics == |
| | + | |
| | + | :* [[Short Circuit]] |
| | + | :* [[Transformer Inrush]] |
| | | | |
| | [[Category:Modelling / Analysis]] | | [[Category:Modelling / Analysis]] |
Introduction
The RL switching / closing transient is one of the most common electrical transients that is encountered in practice, and is also the basis for the computation of short circuit currents.
Derivation
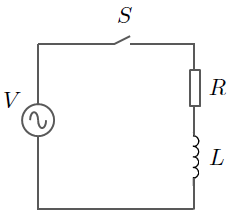
Figure 1. Basic RL switching circuit
Consider the basic switching circuit in the figure to the right, consisting of an AC voltage source V, a switch S, a resistance R and an inductance L (all ideal circuit elements). At time  , the switch S will close and complete the circuit. Suppose the voltage source can be characterised as a sinusoid (as a function of time):
, the switch S will close and complete the circuit. Suppose the voltage source can be characterised as a sinusoid (as a function of time):

Where  is an arbitrary phase angle to capture the time of switching.
is an arbitrary phase angle to capture the time of switching.
At the point of switching, the voltage is given by Kirchhoff's voltage law:

The current  must reach a steady state current of:
must reach a steady state current of:
 ... Equ. (1)
... Equ. (1)
And have a steady state power factor:

However, at  ,
,  and the inductance
and the inductance  will prevent the circuit from reaching the steady-state current instantaneously. Therefore, there must be some transient that will provide a continuous transition path from
will prevent the circuit from reaching the steady-state current instantaneously. Therefore, there must be some transient that will provide a continuous transition path from  to the steady-state current
to the steady-state current  .
.
Equation (1) can be re-written as follows:
![{\displaystyle V_{m}\left[\sin(\omega t)\cos \theta +\cos(\omega t)\sin \theta \right]=RI(t)+L{\frac {dI(t)}{dt}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76896a97860adcd8b146a10295154b247ec6f015)
Taking the Laplace transform of both sides, we get:

We assume that the initial current  , so therefore re-arranging the equation above we get:
, so therefore re-arranging the equation above we get:

![{\displaystyle ={\frac {V_{m}}{L}}\left[{\frac {\omega \cos \theta }{(s^{2}+\omega ^{2})({\frac {R}{L}}+s)}}+{\frac {s\sin \theta }{(s^{2}+\omega ^{2})({\frac {R}{L}}+s)}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18a6d108598101b699ef707c78ce93c154d643b0) ... Equ. (2)
... Equ. (2)
It can be shown that the expression  can be simplified as follows:
can be simplified as follows:

Therefore, the inverse Laplace transforms of the terms in Equation (2) can be evaluated in a fairly straightforward manner:
1st term: ![{\displaystyle {\mathcal {L}}^{-1}\left[{\frac {\omega \cos \theta }{(s^{2}+\omega ^{2})({\frac {R}{L}}+s)}}\right]={\frac {\omega \cos \theta }{\left({\frac {R}{L}}\right)^{2}+\omega ^{2}}}\left[e^{-{\frac {R}{L}}t}-\cos(\omega t)+{\frac {R}{\omega L}}\sin(\omega t)\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0867a8906955333c2fd1cc91ad2d21e649a4d6c9)
2nd term: ![{\displaystyle {\mathcal {L}}^{-1}\left[{\frac {s\sin \theta }{(s^{2}+\omega ^{2})({\frac {R}{L}}+s)}}\right]={\frac {\sin \theta }{\left({\frac {R}{L}}\right)^{2}+\omega ^{2}}}\left[-{\frac {R}{L}}e^{-{\frac {R}{L}}t}+\omega \sin(\omega t)+{\frac {R}{L}}\cos(\omega t)\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e766eb2d9850cf1544d0ff2ad1f91bbcefdddbf)
Combining the two terms together (and including the constants), we get the transient current:
![{\displaystyle I(t)={\frac {V_{m}}{L\left({\frac {R}{L}}\right)^{2}+\omega ^{2}}}\left[(\omega \cos \theta -{\frac {R}{L}}\sin \theta )e^{-{\frac {R}{L}}t}+({\frac {R}{L}}\cos \theta +\omega \sin \theta )\sin(\omega t)-(\omega \cos \theta -{\frac {R}{L}}\sin \theta )\cos(\omega t)\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd76a98170a6d59416f76b49793c05a44f05e5b1) ... Equ. (3)
... Equ. (3)
Earlier, we found that the steady state power factor is:

This can be re-arranged as follows:

Likewise, the sine of the power angle is:

Using these two equations above, we can simplify Equation (3) even further:
![{\displaystyle I(t)={\frac {V_{m}{\sqrt {({\frac {R}{L}})^{2}+\omega ^{2}}}}{L\left[\left({\frac {R}{L}}\right)^{2}+\omega ^{2}\right]}}\left[(\cos \theta \sin \phi _{s}-\sin \theta \cos \phi _{s})e^{-{\frac {R}{L}}t}+(\cos \theta \cos \phi _{s}+\sin \theta \sin \phi _{s})\sin(\omega t)-(\cos \theta \sin \phi _{s}-\sin \theta \cos \phi _{s})\cos(\omega t)\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/021f420c04faee1f0d5c9631e41683c5fc39c238)
Using some angle sum and difference trigonometric identities, we get:
![{\displaystyle I(t)={\frac {V_{m}}{\sqrt {(R^{2}+\omega ^{2}L^{2}}}}\left[(-\sin(\theta -\phi _{s})e^{-{\frac {R}{L}}t}+(\cos \theta \cos \phi _{s}+\sin(\theta -\phi _{s})\sin(\omega t)+(\cos(\theta -\phi _{s})\cos(\omega t)\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f648667592bdeba7fec15c95f890ad18afa20185)
Simplifying again with the same trig identities, we get the final equation:
![{\displaystyle I(t)={\frac {V_{m}}{\sqrt {(R^{2}+\omega ^{2}L^{2}}}}\left[(\sin(\omega t+\theta -\phi _{s})-\sin(\theta -\phi _{s})e^{-{\frac {R}{L}}t}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfe9a7927df85065df135829a9fff1ae829e4349) ... Equ. (4)
... Equ. (4)
Interpretation
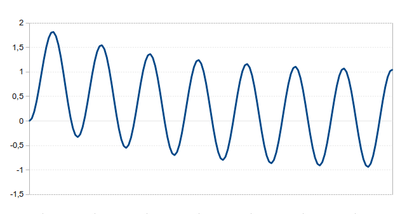
Figure 2. RL switching transient current
The figure right depicts a plot of the transient current in Equation (4) for the parameters R/L = 40 and switching angle  = 0o. Here we see the classic transient current waveform for an RL switching (closing) circuit with the time constant R/L.
= 0o. Here we see the classic transient current waveform for an RL switching (closing) circuit with the time constant R/L.
Related Topics











![{\displaystyle V_{m}\left[\sin(\omega t)\cos \theta +\cos(\omega t)\sin \theta \right]=RI(t)+L{\frac {dI(t)}{dt}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76896a97860adcd8b146a10295154b247ec6f015)


![{\displaystyle ={\frac {V_{m}}{L}}\left[{\frac {\omega \cos \theta }{(s^{2}+\omega ^{2})({\frac {R}{L}}+s)}}+{\frac {s\sin \theta }{(s^{2}+\omega ^{2})({\frac {R}{L}}+s)}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18a6d108598101b699ef707c78ce93c154d643b0)


![{\displaystyle {\mathcal {L}}^{-1}\left[{\frac {\omega \cos \theta }{(s^{2}+\omega ^{2})({\frac {R}{L}}+s)}}\right]={\frac {\omega \cos \theta }{\left({\frac {R}{L}}\right)^{2}+\omega ^{2}}}\left[e^{-{\frac {R}{L}}t}-\cos(\omega t)+{\frac {R}{\omega L}}\sin(\omega t)\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0867a8906955333c2fd1cc91ad2d21e649a4d6c9)
![{\displaystyle {\mathcal {L}}^{-1}\left[{\frac {s\sin \theta }{(s^{2}+\omega ^{2})({\frac {R}{L}}+s)}}\right]={\frac {\sin \theta }{\left({\frac {R}{L}}\right)^{2}+\omega ^{2}}}\left[-{\frac {R}{L}}e^{-{\frac {R}{L}}t}+\omega \sin(\omega t)+{\frac {R}{L}}\cos(\omega t)\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e766eb2d9850cf1544d0ff2ad1f91bbcefdddbf)
![{\displaystyle I(t)={\frac {V_{m}}{L\left({\frac {R}{L}}\right)^{2}+\omega ^{2}}}\left[(\omega \cos \theta -{\frac {R}{L}}\sin \theta )e^{-{\frac {R}{L}}t}+({\frac {R}{L}}\cos \theta +\omega \sin \theta )\sin(\omega t)-(\omega \cos \theta -{\frac {R}{L}}\sin \theta )\cos(\omega t)\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd76a98170a6d59416f76b49793c05a44f05e5b1)



![{\displaystyle I(t)={\frac {V_{m}{\sqrt {({\frac {R}{L}})^{2}+\omega ^{2}}}}{L\left[\left({\frac {R}{L}}\right)^{2}+\omega ^{2}\right]}}\left[(\cos \theta \sin \phi _{s}-\sin \theta \cos \phi _{s})e^{-{\frac {R}{L}}t}+(\cos \theta \cos \phi _{s}+\sin \theta \sin \phi _{s})\sin(\omega t)-(\cos \theta \sin \phi _{s}-\sin \theta \cos \phi _{s})\cos(\omega t)\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/021f420c04faee1f0d5c9631e41683c5fc39c238)
![{\displaystyle I(t)={\frac {V_{m}}{\sqrt {(R^{2}+\omega ^{2}L^{2}}}}\left[(-\sin(\theta -\phi _{s})e^{-{\frac {R}{L}}t}+(\cos \theta \cos \phi _{s}+\sin(\theta -\phi _{s})\sin(\omega t)+(\cos(\theta -\phi _{s})\cos(\omega t)\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f648667592bdeba7fec15c95f890ad18afa20185)
![{\displaystyle I(t)={\frac {V_{m}}{\sqrt {(R^{2}+\omega ^{2}L^{2}}}}\left[(\sin(\omega t+\theta -\phi _{s})-\sin(\theta -\phi _{s})e^{-{\frac {R}{L}}t}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfe9a7927df85065df135829a9fff1ae829e4349)

