This article describes the steady-state or frequency domain distributed parameter line model. By steady-state, we mean that the voltage and current along the line are steady and do not change with time.
Single-Phase Distributed Parameter Model
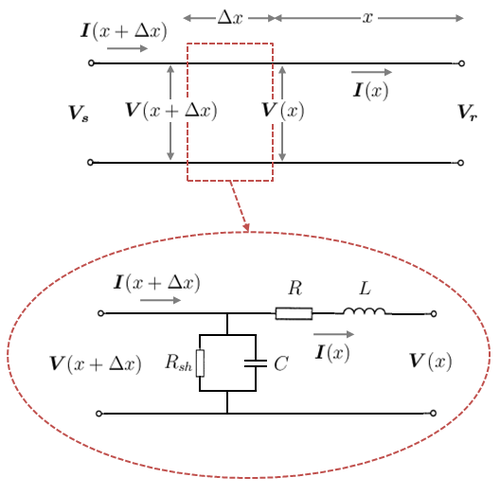
Figure 1. Distributed parameter line model (single-phase): Overall line representation (top); Model for a small line segment (bottom)
In a real transmission line, the R, L and C circuit elements are not lumped together, but are uniformly distributed along the length of the line. In order to capture the distributed nature of the circuit parameters, consider the single-phase line model in Figure 1. In particular, consider a small line segment of length  metres, which is located at a distance
metres, which is located at a distance  metres from the receiving end bus.
metres from the receiving end bus.
The top diagram of Figure 1 shows the complete transmission line and the small line segment is represented by the dotted box. The bottom diagram is an expanded view of the line segment showing a typical line segment model with series and shunt circuit elements. The series elements can be represented as an impedance and the shunt elements can be represented as an admittance as follows:


Where  is the series resistance (
is the series resistance ( )
)
 is the series reactance (
is the series reactance ( )
) is the shunt conductance (
is the shunt conductance ( )
) is the shunt susceptance (
is the shunt susceptance ( )
)
Note that the impedance and admittance are denoted in per-length values (i.e. per metre). Therefore, the series impedance of a line segment of length  metres is
metres is  . The same logic applies for the shunt admittance.
. The same logic applies for the shunt admittance.
Derivation of Voltage and Current Equations
Analysing this circuit using Kirchhoff's voltage law:

Re-arranging this equation, we get:

The left-hand side is Newton's difference quotient and the limit as  is by definition the derivative of
is by definition the derivative of  , i.e.
, i.e.
 ... Equ. (1)
... Equ. (1)
Similarly, analysing the circuit using Kirchhoff's current law:

Re-arranging this equation, we get:

Taking the limit of both sides as  :
:
 ... Equ. (2)
... Equ. (2)
Differentiating Equations (1) and (2) again with respect to  , we get:
, we get:


We can re-substitute Equations (1) and (2) into the above to get:
 ... Equ. (3)
... Equ. (3)
 ... Equ. (4)
... Equ. (4)
The pair of equations above can be re-arranged to form homogenous second-order linear ordinary differential equations, i.e.

The general solution to this differential equation is:

Where  is known as the propagation constant (with units
is known as the propagation constant (with units  )
)
Plugging this solution back into Equ. (1), we can also solve for  , i.e.
, i.e.
![{\displaystyle {\frac {d}{dx}}\left[A_{1}e^{{\boldsymbol {\gamma }}x}+A_{2}e^{-{\boldsymbol {\gamma }}x}\right]={\boldsymbol {z}}{\boldsymbol {I}}(x)\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/255377442f42c2f7b03515c5a8875d56e490d97b)

Where  is known as the characteristic impedance or surge impedance (with units
is known as the characteristic impedance or surge impedance (with units  )
)
We can solve for the constants  and
and  by using the boundary conditions at the receiving end of the line, i.e. at the receiving end,
by using the boundary conditions at the receiving end of the line, i.e. at the receiving end,  ,
,  and
and  . The solution is as follows (see the full derivation here):
. The solution is as follows (see the full derivation here):


Substituting these constants, we get the final distributed parameter transmission line equations:
 ... Equ. (5)
... Equ. (5)
 ... Equ. (6)
... Equ. (6)
Hyperbolic Form of Transmission Line Equations
Equations (5) and (6) can be re-arranged as follows:


Given the exponential forms of the hyperbolic functions  and
and  :
:


We can substitute these into the transmission line equations to get the well-known hyperbolic form of the equations:


For a line of length  metres, the ABCD parameters of the above equations can be represented in matrix form as follows:
metres, the ABCD parameters of the above equations can be represented in matrix form as follows:
![{\displaystyle \left[{\begin{matrix}{\boldsymbol {V_{s}}}\\\\{\boldsymbol {I_{s}}}\end{matrix}}\right]=\left[{\begin{matrix}\cosh({\boldsymbol {\gamma }}l)&{\boldsymbol {Z}}_{c}\sinh({\boldsymbol {\gamma }}l)\\\\{\frac {1}{{\boldsymbol {Z}}_{c}}}sinh({\boldsymbol {\gamma }}l)&\cosh({\boldsymbol {\gamma }}l)\end{matrix}}\right]\left[{\begin{matrix}{\boldsymbol {V_{r}}}\\\\{\boldsymbol {I_{r}}}\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/84c751fe40fbb9e608b1835a0512c90917157eaa)
where the sending end quantities are  and
and 
Multi-conductor Distributed Parameter Model
The distributed parameter model can be extended to a multi-conductor line of n conductors by replacing the voltage and current phasors with  vectors, e.g. for a three-phase, three-conductor line:
vectors, e.g. for a three-phase, three-conductor line:
![{\displaystyle {\boldsymbol {V}}=\left[{\begin{matrix}{\boldsymbol {V_{a}}}(x)\\{\boldsymbol {V_{b}}}(x)\\{\boldsymbol {V_{c}}}(x)\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/871052202d722e67f2acf86ae5ed6b6ce43e1c62) ,
, ![{\displaystyle {\boldsymbol {I}}=\left[{\begin{matrix}{\boldsymbol {I_{a}}}(x)\\{\boldsymbol {I_{b}}}(x)\\{\boldsymbol {I_{c}}}(x)\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ff8ccbddee539e86eddf94657518a60017c5093)
And the impedance and admittance with  complex matrices, e.g. for a three-phase, three-conductor line:
complex matrices, e.g. for a three-phase, three-conductor line:
![{\displaystyle [Z]=\left[{\begin{matrix}Z_{aa}&Z_{ab}&Z_{ac}\\Z_{ba}&Z_{bb}&Z_{bc}\\Z_{ca}&Z_{cb}&Z_{cc}\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2693bea7e112293f494843d1c33f490713b3257)
![{\displaystyle [Y]=\left[{\begin{matrix}Y_{aa}&Y_{ab}&Y_{ac}\\Y_{ba}&Y_{bb}&Y_{bc}\\Y_{ca}&Y_{cb}&Y_{cc}\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0bc823734ff641934d2418973702875ec6fbc5b5)
Equations (1) and (2) above in the single-phase model can now be re-written in the multi-conductor model as:
![{\displaystyle {\frac {d{\boldsymbol {V}}}{dx}}=[Z]{\boldsymbol {I}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/801c224d4fd939c4053246e15a1f43b66fce3f2b) ... Equ. (7)
... Equ. (7)
![{\displaystyle {\frac {d{\boldsymbol {I}}}{dx}}=[Y]{\boldsymbol {V}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2c909fc82c160cd797af08628b771de91832317) ... Equ. (8)
... Equ. (8)
Differentiating these equations with respect to  , we get:
, we get:
![{\displaystyle {\frac {d^{2}{\boldsymbol {V}}}{dx^{2}}}=[Z]{\frac {d{\boldsymbol {I}}}{dx}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52b83da23d71dc726f4a38fbe1ef33475ff6a2af) ... Equ. (9)
... Equ. (9)
![{\displaystyle {\frac {d^{2}{\boldsymbol {I}}}{dx^{2}}}=[Y]{\frac {d{\boldsymbol {V}}}{dx}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f01eb5addcd120c9d88b388b7edb557f493c53b) ... Equ. (10)
... Equ. (10)
Substituting Equ. (8) into Equ. (9) and Equ. (7) into Equ. (10), we end up with the multi-conductor equivalent of equations (3) and (4):
![{\displaystyle {\frac {d^{2}{\boldsymbol {V}}}{dx^{2}}}=[Z][Y]{\boldsymbol {V}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0834f342c6e39469b0ce1224cf905ee4f4795cf3) ... Equ. (11)
... Equ. (11)
![{\displaystyle {\frac {d^{2}{\boldsymbol {I}}}{dx^{2}}}=[Y][Z]{\boldsymbol {I}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d436256d63b51478243388157773c3535d05e58f) ... Equ. (12)
... Equ. (12)
The issue with the multi-conductor case is that because the matrices [Z] and [Y] are full, then their product [Z][Y] or [Y][Z] is also full. For example, if we were to expand out Equ. (11):
![{\displaystyle \left[{\begin{matrix}{\frac {d^{2}{\boldsymbol {V_{a}}}(x)}{dx^{2}}}\\\\{\frac {d^{2}{\boldsymbol {V_{b}}}(x)}{dx^{2}}}\\\\{\frac {d^{2}{\boldsymbol {V_{c}}}(x)}{dx^{2}}}\end{matrix}}\right]=\left[{\begin{matrix}Z_{aa}&Z_{ab}&Z_{ac}\\Z_{ba}&Z_{bb}&Z_{bc}\\Z_{ca}&Z_{cb}&Z_{cc}\end{matrix}}\right]\left[{\begin{matrix}Y_{aa}&Y_{ab}&Y_{ac}\\Y_{ba}&Y_{bb}&Y_{bc}\\Y_{ca}&Y_{cb}&Y_{cc}\end{matrix}}\right]\left[{\begin{matrix}{\boldsymbol {V_{a}}}(x)\\{\boldsymbol {V_{b}}}(x)\\{\boldsymbol {V_{c}}}(x)\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f64cc71dd3b397dc0c779bdcdab0b7d192d934c1)
The first line of the system of equations above can be expanded as follows:

Unlike in the single-phase case above, there is no closed-form general solution to this second-order differential equation (because of the cross-coupling between phases). The so-called modal transformation is required to decouple the phases from equations (11) and (12).
Modal Transformation
The modal transformation is a technique for decoupling the phases from equations (11) and (12) based on an Eigenvalue decomposition. In this section, we will develop the modal transformation from first principles. Alternative derivations can be found in [1], [2] and [3].
Consider linear transforms of the voltage and current vectors denoted  and
and  , where by convention, the subscripts change from phases (abc) to modes (012), i.e. for a three-phase, three-conductor line:
, where by convention, the subscripts change from phases (abc) to modes (012), i.e. for a three-phase, three-conductor line:
![{\displaystyle {\boldsymbol {V'}}=\left[{\begin{matrix}{\boldsymbol {V_{0}}}(x)\\{\boldsymbol {V_{1}}}(x)\\{\boldsymbol {V_{2}}}(x)\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b492a70b9af015322f0758d5d494eacd3abc2d17) ,
, ![{\displaystyle {\boldsymbol {I'}}=\left[{\begin{matrix}{\boldsymbol {I_{0}}}(x)\\{\boldsymbol {I_{1}}}(x)\\{\boldsymbol {I_{2}}}(x)\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41f924c9f70fca65c12bc3bf3d15d28a4e3cccd1)
Suppose that the original quantities are related to the transformed quantities as follows:
![{\displaystyle {\boldsymbol {V}}=[T_{v}]{\boldsymbol {V'}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d572f533693476ab9710b03596b84a89a9903a34) ... Equ. (13)
... Equ. (13)
![{\displaystyle {\boldsymbol {I}}=[T_{i}]{\boldsymbol {I'}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5642e4afa0e407d92a12133f5101d04e8eade5e) ... Equ. (14)
... Equ. (14)
Where ![{\displaystyle [T_{v}]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2838c4c191c867ff1627123f06beedcb05c2d2bd) and
and ![{\displaystyle [T_{i}]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e29111c511b58a6f5ac4f689dacee1e8f3027e50) are
are  transformation matrices. We won't define the transformation matrices just yet, but it will become obvious later on that they are actually the eigenvectors of
transformation matrices. We won't define the transformation matrices just yet, but it will become obvious later on that they are actually the eigenvectors of ![{\displaystyle [Z][Y]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e334df9f96e8de319adfbab65811e92d5ea166b4) and
and ![{\displaystyle [Y][Z]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19bd911f0caee63923881b4ec5347c0c2eb6d6a6) respectively.
respectively.
Substituting these transformed quantities into equations (7) and (8):
![{\displaystyle {\frac {d[T_{v}]{\boldsymbol {V'}}}{dx}}=[Z][T_{i}]{\boldsymbol {I'}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73dba4e37651a5e08078be2ed2e55894878ad1fe)
![{\displaystyle {\frac {d[T_{i}]{\boldsymbol {I'}}}{dx}}=[Y][T_{v}]{\boldsymbol {V'}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3d2ec4dd27912bf2602a0a68ff744a013e690de)
Supposing that the transformation matrices ![{\displaystyle [T_{v}]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2838c4c191c867ff1627123f06beedcb05c2d2bd) and
and ![{\displaystyle [T_{i}]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e29111c511b58a6f5ac4f689dacee1e8f3027e50) are independent of x, we can re-arrange the equations above as follows:
are independent of x, we can re-arrange the equations above as follows:
![{\displaystyle {\frac {d{\boldsymbol {V'}}}{dx}}=[T_{v}]^{-1}[Z][T_{i}]{\boldsymbol {I'}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2b72bde149cf4b110b56a2060dd0ffa1149581a)
![{\displaystyle {\frac {d{\boldsymbol {I'}}}{dx}}=[T_{i}]^{-1}[Y][T_{v}]{\boldsymbol {V'}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d8f352cb8fe0fba90cf7be32c91991ba4e2d596)
Following the same procedure as before, i.e. differentiating the equations by x and substituting, we end up with:
![{\displaystyle {\frac {d^{2}{\boldsymbol {V'}}}{dx^{2}}}=[T_{v}]^{-1}[Z][Y][T_{v}]{\boldsymbol {V'}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c3f7fc3380e9b95cc41782d3b5f4a14393d34a1) ... Equ. (15)
... Equ. (15)
![{\displaystyle {\frac {d^{2}{\boldsymbol {I'}}}{dx^{2}}}=[T_{i}]^{-1}[Y][Z][T_{i}]{\boldsymbol {I'}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7291bc83736f457c4c0974028100dbcda367a6af) ... Equ. (16)
... Equ. (16)
In order for us to decouple the phases in equations (15) and (16), we need ![{\displaystyle [T_{v}]^{-1}[Z][Y][T_{v}]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/228fa2c2dd6af51439fdcc203f93cd394c8227ee) and
and ![{\displaystyle [T_{i}]^{-1}[Y][Z][T_{i}]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8591fafcfd9df048b108e88c17d7b37e2b216de) to be diagonal matrices, i.e.
to be diagonal matrices, i.e.
![{\displaystyle diag({\boldsymbol {\lambda _{v}}})=[T_{v}]^{-1}[Z][Y][T_{v}]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29ff7411256d9d454d09876345319c90e964a9a8)
![{\displaystyle diag({\boldsymbol {\lambda _{i}}})=[T_{i}]^{-1}[Y][Z][T_{i}]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4b599805f6553befe0578bb7801293eff948e51)
It is apparent from inspection that the transformation matrix ![{\displaystyle [T_{v}]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2838c4c191c867ff1627123f06beedcb05c2d2bd) and diagonal matrix
and diagonal matrix  are the eigenvectors and eigenvalues of
are the eigenvectors and eigenvalues of ![{\displaystyle [Z][Y]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e334df9f96e8de319adfbab65811e92d5ea166b4) respectively.
respectively.
Similarly, ![{\displaystyle [T_{i}]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e29111c511b58a6f5ac4f689dacee1e8f3027e50) and
and  are the eigenvectors and eigenvalues of
are the eigenvectors and eigenvalues of ![{\displaystyle [Y][Z]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19bd911f0caee63923881b4ec5347c0c2eb6d6a6) .
.
Furthermore, since the matrices ![{\displaystyle [Z]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5067b5d6d581b19e078d8c1d5a0b97bb0a373a5b) and
and ![{\displaystyle [Y]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01412c6c505c0e62440bd89cb84c00de04d6da8d) are both symmetric, then
are both symmetric, then ![{\displaystyle [Z][Y]=\left([Y][Z]\right)^{T}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32d4d42d56f7fde45a193f609002c70d42928aa4) . We know that the eigenvalues of a matrix and its transpose are the same, so therefore
. We know that the eigenvalues of a matrix and its transpose are the same, so therefore ![{\displaystyle [Z][Y]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e334df9f96e8de319adfbab65811e92d5ea166b4) and
and ![{\displaystyle [Y][Z]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19bd911f0caee63923881b4ec5347c0c2eb6d6a6) also share the same eigenvalues, i.e.
also share the same eigenvalues, i.e.

We can now re-write equations (15) and (16) as follows:
![{\displaystyle \left[{\begin{matrix}{\frac {d^{2}{\boldsymbol {V_{0}}}(x)}{dx^{2}}}\\\\{\frac {d^{2}{\boldsymbol {V_{1}}}(x)}{dx^{2}}}\\\\{\frac {d^{2}{\boldsymbol {V_{2}}}(x)}{dx^{2}}}\end{matrix}}\right]=\left[{\begin{matrix}\lambda _{0}&&\\&\lambda _{1}&\\&&\lambda _{2}\end{matrix}}\right]\left[{\begin{matrix}{\boldsymbol {V_{0}}}(x)\\{\boldsymbol {V_{1}}}(x)\\{\boldsymbol {V_{2}}}(x)\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4efdff2d0983233cfb0df9cf9d30638fe377e92) ... Equ. (17)
... Equ. (17)
![{\displaystyle \left[{\begin{matrix}{\frac {d^{2}{\boldsymbol {I_{0}}}(x)}{dx^{2}}}\\\\{\frac {d^{2}{\boldsymbol {I_{1}}}(x)}{dx^{2}}}\\\\{\frac {d^{2}{\boldsymbol {I_{2}}}(x)}{dx^{2}}}\end{matrix}}\right]=\left[{\begin{matrix}\lambda _{0}&&\\&\lambda _{1}&\\&&\lambda _{2}\end{matrix}}\right]\left[{\begin{matrix}{\boldsymbol {I_{0}}}(x)\\{\boldsymbol {I_{1}}}(x)\\{\boldsymbol {I_{2}}}(x)\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3cfbfea0bed0f738d6612521e6f8c41fa0b7d2e0) ... Equ. (18)
... Equ. (18)
Recall from the single-phase case that the propagation constant is defined as  . In multi-conductor matrix form, this can be written as a propagation matrix
. In multi-conductor matrix form, this can be written as a propagation matrix ![{\displaystyle [\Gamma ]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be4e5ebc00e453c3ee907ccae08dc18a06ae7169) as follows:
as follows:
![{\displaystyle [\Gamma ]=([Z][Y])^{\frac {1}{2}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cfe8365858c39b878dc89392b6dc184d1c551e79)
Let the eigenvalues of the propagation matrix ![{\displaystyle [\Gamma ]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be4e5ebc00e453c3ee907ccae08dc18a06ae7169) be
be  .
.
A property of eigenvalues is that if matrix  has the eigenvalues
has the eigenvalues  , then matrix
, then matrix  has the eigenvalues
has the eigenvalues  .
.
Therefore, since  are the eigenvalues of
are the eigenvalues of ![{\displaystyle [Z][Y]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e334df9f96e8de319adfbab65811e92d5ea166b4) and
and  are the eigenvalues of
are the eigenvalues of ![{\displaystyle ([Z][Y])^{\frac {1}{2}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13a34dd1513f8c825e7c19aedc354cd7a68c7272) , we can say that:
, we can say that:
![{\displaystyle \left[{\begin{matrix}\lambda _{0}&&\\&\lambda _{1}&\\&&\lambda _{2}\end{matrix}}\right]=\left[{\begin{matrix}\gamma _{0}^{2}&&\\&\gamma _{1}^{2}&\\&&\gamma _{2}^{2}\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f55864455a52d81988ad8d3f5d6816624328a28b)
We can now re-write equations (17) and (18) as follows:
![{\displaystyle \left[{\begin{matrix}{\frac {d^{2}{\boldsymbol {V_{0}}}(x)}{dx^{2}}}\\\\{\frac {d^{2}{\boldsymbol {V_{1}}}(x)}{dx^{2}}}\\\\{\frac {d^{2}{\boldsymbol {V_{2}}}(x)}{dx^{2}}}\end{matrix}}\right]=\left[{\begin{matrix}\gamma _{0}^{2}&&\\&\gamma _{1}^{2}&\\&&\gamma _{2}^{2}\end{matrix}}\right]\left[{\begin{matrix}{\boldsymbol {V_{0}}}(x)\\{\boldsymbol {V_{1}}}(x)\\{\boldsymbol {V_{2}}}(x)\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c4f1692efe73d0fc06bb578926c2c0405e822d0) ... Equ. (19)
... Equ. (19)
![{\displaystyle \left[{\begin{matrix}{\frac {d^{2}{\boldsymbol {I_{0}}}(x)}{dx^{2}}}\\\\{\frac {d^{2}{\boldsymbol {I_{1}}}(x)}{dx^{2}}}\\\\{\frac {d^{2}{\boldsymbol {I_{2}}}(x)}{dx^{2}}}\end{matrix}}\right]=\left[{\begin{matrix}\gamma _{0}^{2}&&\\&\gamma _{1}^{2}&\\&&\gamma _{2}^{2}\end{matrix}}\right]\left[{\begin{matrix}{\boldsymbol {I_{0}}}(x)\\{\boldsymbol {I_{1}}}(x)\\{\boldsymbol {I_{2}}}(x)\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79a8d5ad1aa78080c552691b014234136cf767cb) ... Equ. (20)
... Equ. (20)
Each of these decoupled modal differential equations above can now be solved using the general solution:



Taking the first derivative of the equations above with respect to x, we get:
![{\displaystyle \left[{\begin{matrix}{\frac {d{\boldsymbol {V_{0}}}(x)}{dx}}\\\\{\frac {d{\boldsymbol {V_{1}}}(x)}{dx}}\\\\{\frac {d{\boldsymbol {V_{2}}}(x)}{dx}}\end{matrix}}\right]=\left[{\begin{matrix}\gamma _{0}&&\\&\gamma _{1}&\\&&\gamma _{2}\end{matrix}}\right]\left[{\begin{matrix}A_{0}e^{\gamma _{0}x}-B_{0}e^{-\gamma _{0}x}\\A_{1}e^{\gamma _{1}x}-B_{1}e^{-\gamma _{1}x}\\A_{2}e^{\gamma _{2}x}-B_{2}e^{-\gamma _{2}x}\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76b56ada7a0cf350267832efa88d8d719626c239) ... Equ. (21)
... Equ. (21)
Let's denote equation (21) above in the following shorthand notation:
![{\displaystyle {\frac {d{\boldsymbol {V'}}}{dx}}=[\gamma ]{\boldsymbol {V_{x}}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d241633a4e742df8f3ef5e117bf4a2b6ba5fc12) ... Equ. (22)
... Equ. (22)
Recall from earlier that:
![{\displaystyle {\frac {d{\boldsymbol {V'}}}{dx}}=[T_{v}]^{-1}[Z][T_{i}]{\boldsymbol {I'}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2b72bde149cf4b110b56a2060dd0ffa1149581a)
Equating this with equation (22) and solving for  , we get:
, we get:
![{\displaystyle {\boldsymbol {V_{x}}}=[\gamma ]^{-1}[T_{v}]^{-1}[Z][T_{i}]{\boldsymbol {I'}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/275bf8c7aec017a91c7e286aa0387f37d9d0273e)
We define the modal characteristic impedance matrix (or modal surge impedance matrix) as:
![{\displaystyle [Z_{c}]=[\gamma ]^{-1}[T_{v}]^{-1}[Z][T_{i}]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/174b5acd622f1354b77ed0580710031967e7fc41) ... Equ. (23)
... Equ. (23)
Using this definition, the modal current vector can be expressed as:
![{\displaystyle {\boldsymbol {I'}}=[Z_{c}]^{-1}{\boldsymbol {V_{x}}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac0dd0b75897294428fb508bd82439a74c5f5ba6) ... Equ. (24)
... Equ. (24)
It can be shown that if ![{\displaystyle [\gamma ]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ddd84a79b861cc494621787894164a6ff3d0c6d) is diagonal, then
is diagonal, then ![{\displaystyle [Z_{c}]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/700664449f444a376039166f3c274346b2afc14b) is also diagonal (see the derivation here). Therefore, when expanded, equation (24) looks like this:
is also diagonal (see the derivation here). Therefore, when expanded, equation (24) looks like this:
![{\displaystyle \left[{\begin{matrix}{\boldsymbol {I_{0}}}(x)\\{\boldsymbol {I_{1}}}(x)\\{\boldsymbol {I_{2}}}(x)\end{matrix}}\right]=\left[{\begin{matrix}{\frac {1}{\boldsymbol {Z_{0}}}}&&\\&{\frac {1}{\boldsymbol {Z_{1}}}}&\\&&{\frac {1}{\boldsymbol {Z_{2}}}}\end{matrix}}\right]\left[{\begin{matrix}A_{0}e^{\gamma _{0}x}-B_{0}e^{-\gamma _{0}x}\\A_{1}e^{\gamma _{1}x}-B_{1}e^{-\gamma _{1}x}\\A_{2}e^{\gamma _{2}x}-B_{2}e^{-\gamma _{2}x}\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06d71d9fe7dbe2d86d86de3eea7fffcf187c7717) ... Equ. (25)
... Equ. (25)
Boundary Conditions
We now have the following six modal equations that we can solve using boundary conditions:
![{\displaystyle \left[{\begin{matrix}{\boldsymbol {V_{0}}}(x)\\{\boldsymbol {V_{1}}}(x)\\{\boldsymbol {V_{2}}}(x)\end{matrix}}\right]=\left[{\begin{matrix}A_{0}e^{\gamma _{0}x}+B_{0}e^{-\gamma _{0}x}\\A_{1}e^{\gamma _{1}x}+B_{1}e^{-\gamma _{1}x}\\A_{2}e^{\gamma _{2}x}+B_{2}e^{-\gamma _{2}x}\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee3fbe383d3c4b7cf7b20f78b4a3d1236be3cc1a)
![{\displaystyle \left[{\begin{matrix}{\boldsymbol {I_{0}}}(x)\\{\boldsymbol {I_{1}}}(x)\\{\boldsymbol {I_{2}}}(x)\end{matrix}}\right]=\left[{\begin{matrix}{\frac {1}{\boldsymbol {Z_{0}}}}&&\\&{\frac {1}{\boldsymbol {Z_{1}}}}&\\&&{\frac {1}{\boldsymbol {Z_{2}}}}\end{matrix}}\right]\left[{\begin{matrix}A_{0}e^{\gamma _{0}x}-B_{0}e^{-\gamma _{0}x}\\A_{1}e^{\gamma _{1}x}-B_{1}e^{-\gamma _{1}x}\\A_{2}e^{\gamma _{2}x}-B_{2}e^{-\gamma _{2}x}\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06d71d9fe7dbe2d86d86de3eea7fffcf187c7717)
The boundary conditions at the receiving end  and
and  must be transformed to modal quantities as follows:
must be transformed to modal quantities as follows:
![{\displaystyle {\boldsymbol {V_{r}}}'=[T_{v}]^{-1}{\boldsymbol {V_{r}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8f48cf8dc7f08eb42a9b4de1220ef2c11b7a37a)
![{\displaystyle {\boldsymbol {I_{r}}}'=[T_{i}]^{-1}{\boldsymbol {I_{r}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c95e82f954eb11b2d683451b62936f0c88f70a9)
At the receiving end (i.e. x = 0), the modal equations reduce as follows:
![{\displaystyle \left[{\begin{matrix}{\boldsymbol {V_{0r}}}\\{\boldsymbol {V_{1r}}}\\{\boldsymbol {V_{2r}}}\end{matrix}}\right]=\left[{\begin{matrix}A_{0}+B_{0}\\A_{1}+B_{1}\\A_{2}+B_{2}\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63e55b12325df1c1175e423a0b4f0bc7d6e8cc38)
![{\displaystyle \left[{\begin{matrix}{\boldsymbol {Z_{0}}}{\boldsymbol {I_{0r}}}\\{\boldsymbol {Z_{1}}}{\boldsymbol {I_{1r}}}\\{\boldsymbol {Z_{2}}}{\boldsymbol {I_{2r}}}\end{matrix}}\right]=\left[{\begin{matrix}A_{0}-B_{0}\\A_{1}-B_{1}\\A_{2}-B_{2}\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24b802af3f9c77d931c5c6a760cd4c4a721bb60b)
Solving for the constants of ![{\displaystyle [A]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6cbf1fb4a9d38c91451b02e34253a0924d53addb) and
and ![{\displaystyle [B]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c69e183a615e7bae607d746d3b7d44b0d8316ff6) :
:
![{\displaystyle \left[{\begin{matrix}A_{0}\\A_{1}\\A_{2}\end{matrix}}\right]={\frac {1}{2}}\left[{\begin{matrix}{\boldsymbol {V_{0r}}}-{\boldsymbol {Z_{0}}}{\boldsymbol {I_{0r}}}\\{\boldsymbol {V_{1r}}}-{\boldsymbol {Z_{1}}}{\boldsymbol {I_{1r}}}\\{\boldsymbol {V_{2r}}}-{\boldsymbol {Z_{2}}}{\boldsymbol {I_{2r}}}\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2227e6be8d0df4e35bc4d63978aa903a702f04ba) ... Equ. (26)
... Equ. (26)
![{\displaystyle \left[{\begin{matrix}B_{0}\\B_{1}\\B_{2}\end{matrix}}\right]={\frac {1}{2}}\left[{\begin{matrix}{\boldsymbol {V_{0r}}}+{\boldsymbol {Z_{0}}}{\boldsymbol {I_{0r}}}\\{\boldsymbol {V_{1r}}}+{\boldsymbol {Z_{1}}}{\boldsymbol {I_{1r}}}\\{\boldsymbol {V_{2r}}}+{\boldsymbol {Z_{2}}}{\boldsymbol {I_{2r}}}\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2544955a8f253cb8711fa21afc354c455f7f619) ... Equ. (27)
... Equ. (27)
These constants can be plugged back into the modal voltage and current equations to get the final expressions:
![{\displaystyle \left[{\begin{matrix}{\boldsymbol {V_{0}}}(x)\\{\boldsymbol {V_{1}}}(x)\\{\boldsymbol {V_{2}}}(x)\end{matrix}}\right]={\frac {1}{2}}\left[{\begin{matrix}({\boldsymbol {V_{0r}}}-{\boldsymbol {Z_{0}}}{\boldsymbol {I_{0r}}})e^{\gamma _{0}x}+({\boldsymbol {V_{0r}}}+{\boldsymbol {Z_{0}}}{\boldsymbol {I_{0r}}})e^{-\gamma _{0}x}\\({\boldsymbol {V_{1r}}}-{\boldsymbol {Z_{1}}}{\boldsymbol {I_{1r}}})e^{\gamma _{1}x}+({\boldsymbol {V_{1r}}}+{\boldsymbol {Z_{1}}}{\boldsymbol {I_{1r}}})e^{-\gamma _{1}x}\\({\boldsymbol {V_{2r}}}-{\boldsymbol {Z_{2}}}{\boldsymbol {I_{2r}}})e^{\gamma _{2}x}+({\boldsymbol {V_{2r}}}+{\boldsymbol {Z_{2}}}{\boldsymbol {I_{2r}}})e^{-\gamma _{2}x}\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d128e988da2836750f0bd0d7fc7a04ae12090d01) ... Equ. (28)
... Equ. (28)
![{\displaystyle \left[{\begin{matrix}{\boldsymbol {I_{0}}}(x)\\{\boldsymbol {I_{1}}}(x)\\{\boldsymbol {I_{2}}}(x)\end{matrix}}\right]=\left[{\begin{matrix}{\frac {1}{2{\boldsymbol {Z_{0}}}}}&&\\&{\frac {1}{2{\boldsymbol {Z_{1}}}}}&\\&&{\frac {1}{2{\boldsymbol {Z_{2}}}}}\end{matrix}}\right]\left[{\begin{matrix}({\boldsymbol {V_{0r}}}-{\boldsymbol {Z_{0}}}{\boldsymbol {I_{0r}}})e^{\gamma _{0}x}-({\boldsymbol {V_{0r}}}+{\boldsymbol {Z_{0}}}{\boldsymbol {I_{0r}}})e^{-\gamma _{0}x}\\({\boldsymbol {V_{1r}}}-{\boldsymbol {Z_{1}}}{\boldsymbol {I_{1r}}})e^{\gamma _{1}x}-({\boldsymbol {V_{1r}}}+{\boldsymbol {Z_{1}}}{\boldsymbol {I_{1r}}})e^{-\gamma _{1}x}\\({\boldsymbol {V_{2r}}}-{\boldsymbol {Z_{2}}}{\boldsymbol {I_{2r}}})e^{\gamma _{2}x}-({\boldsymbol {V_{2r}}}+{\boldsymbol {Z_{2}}}{\boldsymbol {I_{2r}}})e^{-\gamma _{2}x}\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/957c0e45f48b0765928daa7a8dbef140e5e15b98) ... Equ. (29)
... Equ. (29)
Hyperbolic Form of Multi-conductor Line Equations
As in the single-phase distributed parameter model, the final modal voltages and currents shown in equations (28) and (29) can be converted to the following hyperbolic forms:
![{\displaystyle \left[{\begin{matrix}{\boldsymbol {V_{0}}}(x)\\{\boldsymbol {V_{1}}}(x)\\{\boldsymbol {V_{2}}}(x)\end{matrix}}\right]=\left[{\begin{matrix}\cosh {(\gamma _{0}x)}&&\\&\cosh {(\gamma _{1}x)}&\\&&\cosh {(\gamma _{2}x)}\end{matrix}}\right]\left[{\begin{matrix}{\boldsymbol {V_{0r}}}\\{\boldsymbol {V_{1r}}}\\{\boldsymbol {V_{2r}}}\end{matrix}}\right]+\left[{\begin{matrix}{\boldsymbol {Z_{0}}}\sinh {(\gamma _{0}x)}&&\\&{\boldsymbol {Z_{1}}}\sinh {(\gamma _{1}x)}&\\&&{\boldsymbol {Z_{2}}}\sinh {(\gamma _{2}x)}\end{matrix}}\right]\left[{\begin{matrix}{\boldsymbol {I_{0r}}}\\{\boldsymbol {I_{1r}}}\\{\boldsymbol {I_{2r}}}\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8acdae43770b8f2308afda1254983d9262310a89) ... Equ. (30)
... Equ. (30)
![{\displaystyle \left[{\begin{matrix}{\boldsymbol {I_{0}}}(x)\\{\boldsymbol {I_{1}}}(x)\\{\boldsymbol {I_{2}}}(x)\end{matrix}}\right]=\left[{\begin{matrix}{\frac {1}{\boldsymbol {Z_{0}}}}\sinh {(\gamma _{0}x)}&&\\&{\frac {1}{\boldsymbol {Z_{1}}}}\sinh {(\gamma _{1}x)}&\\&&{\frac {1}{\boldsymbol {Z_{2}}}}\sinh {(\gamma _{2}x)}\end{matrix}}\right]\left[{\begin{matrix}{\boldsymbol {V_{0r}}}\\{\boldsymbol {V_{1r}}}\\{\boldsymbol {V_{2r}}}\end{matrix}}\right]+\left[{\begin{matrix}\cosh {(\gamma _{0}x)}&&\\&\cosh {(\gamma _{1}x)}&\\&&\cosh {(\gamma _{2}x)}\end{matrix}}\right]\left[{\begin{matrix}{\boldsymbol {I_{0r}}}\\{\boldsymbol {I_{1r}}}\\{\boldsymbol {I_{2r}}}\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce6aa3521ed9d631b95061b94b772b9988fd79a8) ... Equ. (31)
... Equ. (31)
Derivations of these forms are straightforward and left to the interested reader to prove.
References
Related Topics





























![{\displaystyle {\frac {d}{dx}}\left[A_{1}e^{{\boldsymbol {\gamma }}x}+A_{2}e^{-{\boldsymbol {\gamma }}x}\right]={\boldsymbol {z}}{\boldsymbol {I}}(x)\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/255377442f42c2f7b03515c5a8875d56e490d97b)





















![{\displaystyle \left[{\begin{matrix}{\boldsymbol {V_{s}}}\\\\{\boldsymbol {I_{s}}}\end{matrix}}\right]=\left[{\begin{matrix}\cosh({\boldsymbol {\gamma }}l)&{\boldsymbol {Z}}_{c}\sinh({\boldsymbol {\gamma }}l)\\\\{\frac {1}{{\boldsymbol {Z}}_{c}}}sinh({\boldsymbol {\gamma }}l)&\cosh({\boldsymbol {\gamma }}l)\end{matrix}}\right]\left[{\begin{matrix}{\boldsymbol {V_{r}}}\\\\{\boldsymbol {I_{r}}}\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/84c751fe40fbb9e608b1835a0512c90917157eaa)



![{\displaystyle {\boldsymbol {V}}=\left[{\begin{matrix}{\boldsymbol {V_{a}}}(x)\\{\boldsymbol {V_{b}}}(x)\\{\boldsymbol {V_{c}}}(x)\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/871052202d722e67f2acf86ae5ed6b6ce43e1c62)
![{\displaystyle {\boldsymbol {I}}=\left[{\begin{matrix}{\boldsymbol {I_{a}}}(x)\\{\boldsymbol {I_{b}}}(x)\\{\boldsymbol {I_{c}}}(x)\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ff8ccbddee539e86eddf94657518a60017c5093)

![{\displaystyle [Z]=\left[{\begin{matrix}Z_{aa}&Z_{ab}&Z_{ac}\\Z_{ba}&Z_{bb}&Z_{bc}\\Z_{ca}&Z_{cb}&Z_{cc}\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2693bea7e112293f494843d1c33f490713b3257)
![{\displaystyle [Y]=\left[{\begin{matrix}Y_{aa}&Y_{ab}&Y_{ac}\\Y_{ba}&Y_{bb}&Y_{bc}\\Y_{ca}&Y_{cb}&Y_{cc}\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0bc823734ff641934d2418973702875ec6fbc5b5)
![{\displaystyle {\frac {d{\boldsymbol {V}}}{dx}}=[Z]{\boldsymbol {I}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/801c224d4fd939c4053246e15a1f43b66fce3f2b)
![{\displaystyle {\frac {d{\boldsymbol {I}}}{dx}}=[Y]{\boldsymbol {V}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2c909fc82c160cd797af08628b771de91832317)
![{\displaystyle {\frac {d^{2}{\boldsymbol {V}}}{dx^{2}}}=[Z]{\frac {d{\boldsymbol {I}}}{dx}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52b83da23d71dc726f4a38fbe1ef33475ff6a2af)
![{\displaystyle {\frac {d^{2}{\boldsymbol {I}}}{dx^{2}}}=[Y]{\frac {d{\boldsymbol {V}}}{dx}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f01eb5addcd120c9d88b388b7edb557f493c53b)
![{\displaystyle {\frac {d^{2}{\boldsymbol {V}}}{dx^{2}}}=[Z][Y]{\boldsymbol {V}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0834f342c6e39469b0ce1224cf905ee4f4795cf3)
![{\displaystyle {\frac {d^{2}{\boldsymbol {I}}}{dx^{2}}}=[Y][Z]{\boldsymbol {I}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d436256d63b51478243388157773c3535d05e58f)
![{\displaystyle \left[{\begin{matrix}{\frac {d^{2}{\boldsymbol {V_{a}}}(x)}{dx^{2}}}\\\\{\frac {d^{2}{\boldsymbol {V_{b}}}(x)}{dx^{2}}}\\\\{\frac {d^{2}{\boldsymbol {V_{c}}}(x)}{dx^{2}}}\end{matrix}}\right]=\left[{\begin{matrix}Z_{aa}&Z_{ab}&Z_{ac}\\Z_{ba}&Z_{bb}&Z_{bc}\\Z_{ca}&Z_{cb}&Z_{cc}\end{matrix}}\right]\left[{\begin{matrix}Y_{aa}&Y_{ab}&Y_{ac}\\Y_{ba}&Y_{bb}&Y_{bc}\\Y_{ca}&Y_{cb}&Y_{cc}\end{matrix}}\right]\left[{\begin{matrix}{\boldsymbol {V_{a}}}(x)\\{\boldsymbol {V_{b}}}(x)\\{\boldsymbol {V_{c}}}(x)\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f64cc71dd3b397dc0c779bdcdab0b7d192d934c1)



![{\displaystyle {\boldsymbol {V'}}=\left[{\begin{matrix}{\boldsymbol {V_{0}}}(x)\\{\boldsymbol {V_{1}}}(x)\\{\boldsymbol {V_{2}}}(x)\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b492a70b9af015322f0758d5d494eacd3abc2d17)
![{\displaystyle {\boldsymbol {I'}}=\left[{\begin{matrix}{\boldsymbol {I_{0}}}(x)\\{\boldsymbol {I_{1}}}(x)\\{\boldsymbol {I_{2}}}(x)\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41f924c9f70fca65c12bc3bf3d15d28a4e3cccd1)
![{\displaystyle {\boldsymbol {V}}=[T_{v}]{\boldsymbol {V'}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d572f533693476ab9710b03596b84a89a9903a34)
![{\displaystyle {\boldsymbol {I}}=[T_{i}]{\boldsymbol {I'}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5642e4afa0e407d92a12133f5101d04e8eade5e)
![{\displaystyle [T_{v}]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2838c4c191c867ff1627123f06beedcb05c2d2bd)
![{\displaystyle [T_{i}]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e29111c511b58a6f5ac4f689dacee1e8f3027e50)
![{\displaystyle [Z][Y]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e334df9f96e8de319adfbab65811e92d5ea166b4)
![{\displaystyle [Y][Z]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19bd911f0caee63923881b4ec5347c0c2eb6d6a6)
![{\displaystyle {\frac {d[T_{v}]{\boldsymbol {V'}}}{dx}}=[Z][T_{i}]{\boldsymbol {I'}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73dba4e37651a5e08078be2ed2e55894878ad1fe)
![{\displaystyle {\frac {d[T_{i}]{\boldsymbol {I'}}}{dx}}=[Y][T_{v}]{\boldsymbol {V'}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3d2ec4dd27912bf2602a0a68ff744a013e690de)
![{\displaystyle {\frac {d{\boldsymbol {V'}}}{dx}}=[T_{v}]^{-1}[Z][T_{i}]{\boldsymbol {I'}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2b72bde149cf4b110b56a2060dd0ffa1149581a)
![{\displaystyle {\frac {d{\boldsymbol {I'}}}{dx}}=[T_{i}]^{-1}[Y][T_{v}]{\boldsymbol {V'}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d8f352cb8fe0fba90cf7be32c91991ba4e2d596)
![{\displaystyle {\frac {d^{2}{\boldsymbol {V'}}}{dx^{2}}}=[T_{v}]^{-1}[Z][Y][T_{v}]{\boldsymbol {V'}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c3f7fc3380e9b95cc41782d3b5f4a14393d34a1)
![{\displaystyle {\frac {d^{2}{\boldsymbol {I'}}}{dx^{2}}}=[T_{i}]^{-1}[Y][Z][T_{i}]{\boldsymbol {I'}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7291bc83736f457c4c0974028100dbcda367a6af)
![{\displaystyle [T_{v}]^{-1}[Z][Y][T_{v}]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/228fa2c2dd6af51439fdcc203f93cd394c8227ee)
![{\displaystyle [T_{i}]^{-1}[Y][Z][T_{i}]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8591fafcfd9df048b108e88c17d7b37e2b216de)
![{\displaystyle diag({\boldsymbol {\lambda _{v}}})=[T_{v}]^{-1}[Z][Y][T_{v}]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29ff7411256d9d454d09876345319c90e964a9a8)
![{\displaystyle diag({\boldsymbol {\lambda _{i}}})=[T_{i}]^{-1}[Y][Z][T_{i}]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4b599805f6553befe0578bb7801293eff948e51)

![{\displaystyle [Z]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5067b5d6d581b19e078d8c1d5a0b97bb0a373a5b)
![{\displaystyle [Y]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01412c6c505c0e62440bd89cb84c00de04d6da8d)
![{\displaystyle [Z][Y]=\left([Y][Z]\right)^{T}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32d4d42d56f7fde45a193f609002c70d42928aa4)

![{\displaystyle \left[{\begin{matrix}{\frac {d^{2}{\boldsymbol {V_{0}}}(x)}{dx^{2}}}\\\\{\frac {d^{2}{\boldsymbol {V_{1}}}(x)}{dx^{2}}}\\\\{\frac {d^{2}{\boldsymbol {V_{2}}}(x)}{dx^{2}}}\end{matrix}}\right]=\left[{\begin{matrix}\lambda _{0}&&\\&\lambda _{1}&\\&&\lambda _{2}\end{matrix}}\right]\left[{\begin{matrix}{\boldsymbol {V_{0}}}(x)\\{\boldsymbol {V_{1}}}(x)\\{\boldsymbol {V_{2}}}(x)\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4efdff2d0983233cfb0df9cf9d30638fe377e92)
![{\displaystyle \left[{\begin{matrix}{\frac {d^{2}{\boldsymbol {I_{0}}}(x)}{dx^{2}}}\\\\{\frac {d^{2}{\boldsymbol {I_{1}}}(x)}{dx^{2}}}\\\\{\frac {d^{2}{\boldsymbol {I_{2}}}(x)}{dx^{2}}}\end{matrix}}\right]=\left[{\begin{matrix}\lambda _{0}&&\\&\lambda _{1}&\\&&\lambda _{2}\end{matrix}}\right]\left[{\begin{matrix}{\boldsymbol {I_{0}}}(x)\\{\boldsymbol {I_{1}}}(x)\\{\boldsymbol {I_{2}}}(x)\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3cfbfea0bed0f738d6612521e6f8c41fa0b7d2e0)
![{\displaystyle [\Gamma ]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be4e5ebc00e453c3ee907ccae08dc18a06ae7169)
![{\displaystyle [\Gamma ]=([Z][Y])^{\frac {1}{2}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cfe8365858c39b878dc89392b6dc184d1c551e79)






![{\displaystyle ([Z][Y])^{\frac {1}{2}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13a34dd1513f8c825e7c19aedc354cd7a68c7272)
![{\displaystyle \left[{\begin{matrix}\lambda _{0}&&\\&\lambda _{1}&\\&&\lambda _{2}\end{matrix}}\right]=\left[{\begin{matrix}\gamma _{0}^{2}&&\\&\gamma _{1}^{2}&\\&&\gamma _{2}^{2}\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f55864455a52d81988ad8d3f5d6816624328a28b)
![{\displaystyle \left[{\begin{matrix}{\frac {d^{2}{\boldsymbol {V_{0}}}(x)}{dx^{2}}}\\\\{\frac {d^{2}{\boldsymbol {V_{1}}}(x)}{dx^{2}}}\\\\{\frac {d^{2}{\boldsymbol {V_{2}}}(x)}{dx^{2}}}\end{matrix}}\right]=\left[{\begin{matrix}\gamma _{0}^{2}&&\\&\gamma _{1}^{2}&\\&&\gamma _{2}^{2}\end{matrix}}\right]\left[{\begin{matrix}{\boldsymbol {V_{0}}}(x)\\{\boldsymbol {V_{1}}}(x)\\{\boldsymbol {V_{2}}}(x)\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c4f1692efe73d0fc06bb578926c2c0405e822d0)
![{\displaystyle \left[{\begin{matrix}{\frac {d^{2}{\boldsymbol {I_{0}}}(x)}{dx^{2}}}\\\\{\frac {d^{2}{\boldsymbol {I_{1}}}(x)}{dx^{2}}}\\\\{\frac {d^{2}{\boldsymbol {I_{2}}}(x)}{dx^{2}}}\end{matrix}}\right]=\left[{\begin{matrix}\gamma _{0}^{2}&&\\&\gamma _{1}^{2}&\\&&\gamma _{2}^{2}\end{matrix}}\right]\left[{\begin{matrix}{\boldsymbol {I_{0}}}(x)\\{\boldsymbol {I_{1}}}(x)\\{\boldsymbol {I_{2}}}(x)\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79a8d5ad1aa78080c552691b014234136cf767cb)



![{\displaystyle \left[{\begin{matrix}{\frac {d{\boldsymbol {V_{0}}}(x)}{dx}}\\\\{\frac {d{\boldsymbol {V_{1}}}(x)}{dx}}\\\\{\frac {d{\boldsymbol {V_{2}}}(x)}{dx}}\end{matrix}}\right]=\left[{\begin{matrix}\gamma _{0}&&\\&\gamma _{1}&\\&&\gamma _{2}\end{matrix}}\right]\left[{\begin{matrix}A_{0}e^{\gamma _{0}x}-B_{0}e^{-\gamma _{0}x}\\A_{1}e^{\gamma _{1}x}-B_{1}e^{-\gamma _{1}x}\\A_{2}e^{\gamma _{2}x}-B_{2}e^{-\gamma _{2}x}\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76b56ada7a0cf350267832efa88d8d719626c239)
![{\displaystyle {\frac {d{\boldsymbol {V'}}}{dx}}=[\gamma ]{\boldsymbol {V_{x}}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d241633a4e742df8f3ef5e117bf4a2b6ba5fc12)

![{\displaystyle {\boldsymbol {V_{x}}}=[\gamma ]^{-1}[T_{v}]^{-1}[Z][T_{i}]{\boldsymbol {I'}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/275bf8c7aec017a91c7e286aa0387f37d9d0273e)
![{\displaystyle [Z_{c}]=[\gamma ]^{-1}[T_{v}]^{-1}[Z][T_{i}]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/174b5acd622f1354b77ed0580710031967e7fc41)
![{\displaystyle {\boldsymbol {I'}}=[Z_{c}]^{-1}{\boldsymbol {V_{x}}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac0dd0b75897294428fb508bd82439a74c5f5ba6)
![{\displaystyle [\gamma ]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ddd84a79b861cc494621787894164a6ff3d0c6d)
![{\displaystyle [Z_{c}]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/700664449f444a376039166f3c274346b2afc14b)
![{\displaystyle \left[{\begin{matrix}{\boldsymbol {I_{0}}}(x)\\{\boldsymbol {I_{1}}}(x)\\{\boldsymbol {I_{2}}}(x)\end{matrix}}\right]=\left[{\begin{matrix}{\frac {1}{\boldsymbol {Z_{0}}}}&&\\&{\frac {1}{\boldsymbol {Z_{1}}}}&\\&&{\frac {1}{\boldsymbol {Z_{2}}}}\end{matrix}}\right]\left[{\begin{matrix}A_{0}e^{\gamma _{0}x}-B_{0}e^{-\gamma _{0}x}\\A_{1}e^{\gamma _{1}x}-B_{1}e^{-\gamma _{1}x}\\A_{2}e^{\gamma _{2}x}-B_{2}e^{-\gamma _{2}x}\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06d71d9fe7dbe2d86d86de3eea7fffcf187c7717)
![{\displaystyle \left[{\begin{matrix}{\boldsymbol {V_{0}}}(x)\\{\boldsymbol {V_{1}}}(x)\\{\boldsymbol {V_{2}}}(x)\end{matrix}}\right]=\left[{\begin{matrix}A_{0}e^{\gamma _{0}x}+B_{0}e^{-\gamma _{0}x}\\A_{1}e^{\gamma _{1}x}+B_{1}e^{-\gamma _{1}x}\\A_{2}e^{\gamma _{2}x}+B_{2}e^{-\gamma _{2}x}\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee3fbe383d3c4b7cf7b20f78b4a3d1236be3cc1a)


![{\displaystyle {\boldsymbol {V_{r}}}'=[T_{v}]^{-1}{\boldsymbol {V_{r}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8f48cf8dc7f08eb42a9b4de1220ef2c11b7a37a)
![{\displaystyle {\boldsymbol {I_{r}}}'=[T_{i}]^{-1}{\boldsymbol {I_{r}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c95e82f954eb11b2d683451b62936f0c88f70a9)
![{\displaystyle \left[{\begin{matrix}{\boldsymbol {V_{0r}}}\\{\boldsymbol {V_{1r}}}\\{\boldsymbol {V_{2r}}}\end{matrix}}\right]=\left[{\begin{matrix}A_{0}+B_{0}\\A_{1}+B_{1}\\A_{2}+B_{2}\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63e55b12325df1c1175e423a0b4f0bc7d6e8cc38)
![{\displaystyle \left[{\begin{matrix}{\boldsymbol {Z_{0}}}{\boldsymbol {I_{0r}}}\\{\boldsymbol {Z_{1}}}{\boldsymbol {I_{1r}}}\\{\boldsymbol {Z_{2}}}{\boldsymbol {I_{2r}}}\end{matrix}}\right]=\left[{\begin{matrix}A_{0}-B_{0}\\A_{1}-B_{1}\\A_{2}-B_{2}\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24b802af3f9c77d931c5c6a760cd4c4a721bb60b)
![{\displaystyle [A]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6cbf1fb4a9d38c91451b02e34253a0924d53addb)
![{\displaystyle [B]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c69e183a615e7bae607d746d3b7d44b0d8316ff6)
![{\displaystyle \left[{\begin{matrix}A_{0}\\A_{1}\\A_{2}\end{matrix}}\right]={\frac {1}{2}}\left[{\begin{matrix}{\boldsymbol {V_{0r}}}-{\boldsymbol {Z_{0}}}{\boldsymbol {I_{0r}}}\\{\boldsymbol {V_{1r}}}-{\boldsymbol {Z_{1}}}{\boldsymbol {I_{1r}}}\\{\boldsymbol {V_{2r}}}-{\boldsymbol {Z_{2}}}{\boldsymbol {I_{2r}}}\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2227e6be8d0df4e35bc4d63978aa903a702f04ba)
![{\displaystyle \left[{\begin{matrix}B_{0}\\B_{1}\\B_{2}\end{matrix}}\right]={\frac {1}{2}}\left[{\begin{matrix}{\boldsymbol {V_{0r}}}+{\boldsymbol {Z_{0}}}{\boldsymbol {I_{0r}}}\\{\boldsymbol {V_{1r}}}+{\boldsymbol {Z_{1}}}{\boldsymbol {I_{1r}}}\\{\boldsymbol {V_{2r}}}+{\boldsymbol {Z_{2}}}{\boldsymbol {I_{2r}}}\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2544955a8f253cb8711fa21afc354c455f7f619)
![{\displaystyle \left[{\begin{matrix}{\boldsymbol {V_{0}}}(x)\\{\boldsymbol {V_{1}}}(x)\\{\boldsymbol {V_{2}}}(x)\end{matrix}}\right]={\frac {1}{2}}\left[{\begin{matrix}({\boldsymbol {V_{0r}}}-{\boldsymbol {Z_{0}}}{\boldsymbol {I_{0r}}})e^{\gamma _{0}x}+({\boldsymbol {V_{0r}}}+{\boldsymbol {Z_{0}}}{\boldsymbol {I_{0r}}})e^{-\gamma _{0}x}\\({\boldsymbol {V_{1r}}}-{\boldsymbol {Z_{1}}}{\boldsymbol {I_{1r}}})e^{\gamma _{1}x}+({\boldsymbol {V_{1r}}}+{\boldsymbol {Z_{1}}}{\boldsymbol {I_{1r}}})e^{-\gamma _{1}x}\\({\boldsymbol {V_{2r}}}-{\boldsymbol {Z_{2}}}{\boldsymbol {I_{2r}}})e^{\gamma _{2}x}+({\boldsymbol {V_{2r}}}+{\boldsymbol {Z_{2}}}{\boldsymbol {I_{2r}}})e^{-\gamma _{2}x}\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d128e988da2836750f0bd0d7fc7a04ae12090d01)
![{\displaystyle \left[{\begin{matrix}{\boldsymbol {I_{0}}}(x)\\{\boldsymbol {I_{1}}}(x)\\{\boldsymbol {I_{2}}}(x)\end{matrix}}\right]=\left[{\begin{matrix}{\frac {1}{2{\boldsymbol {Z_{0}}}}}&&\\&{\frac {1}{2{\boldsymbol {Z_{1}}}}}&\\&&{\frac {1}{2{\boldsymbol {Z_{2}}}}}\end{matrix}}\right]\left[{\begin{matrix}({\boldsymbol {V_{0r}}}-{\boldsymbol {Z_{0}}}{\boldsymbol {I_{0r}}})e^{\gamma _{0}x}-({\boldsymbol {V_{0r}}}+{\boldsymbol {Z_{0}}}{\boldsymbol {I_{0r}}})e^{-\gamma _{0}x}\\({\boldsymbol {V_{1r}}}-{\boldsymbol {Z_{1}}}{\boldsymbol {I_{1r}}})e^{\gamma _{1}x}-({\boldsymbol {V_{1r}}}+{\boldsymbol {Z_{1}}}{\boldsymbol {I_{1r}}})e^{-\gamma _{1}x}\\({\boldsymbol {V_{2r}}}-{\boldsymbol {Z_{2}}}{\boldsymbol {I_{2r}}})e^{\gamma _{2}x}-({\boldsymbol {V_{2r}}}+{\boldsymbol {Z_{2}}}{\boldsymbol {I_{2r}}})e^{-\gamma _{2}x}\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/957c0e45f48b0765928daa7a8dbef140e5e15b98)
![{\displaystyle \left[{\begin{matrix}{\boldsymbol {V_{0}}}(x)\\{\boldsymbol {V_{1}}}(x)\\{\boldsymbol {V_{2}}}(x)\end{matrix}}\right]=\left[{\begin{matrix}\cosh {(\gamma _{0}x)}&&\\&\cosh {(\gamma _{1}x)}&\\&&\cosh {(\gamma _{2}x)}\end{matrix}}\right]\left[{\begin{matrix}{\boldsymbol {V_{0r}}}\\{\boldsymbol {V_{1r}}}\\{\boldsymbol {V_{2r}}}\end{matrix}}\right]+\left[{\begin{matrix}{\boldsymbol {Z_{0}}}\sinh {(\gamma _{0}x)}&&\\&{\boldsymbol {Z_{1}}}\sinh {(\gamma _{1}x)}&\\&&{\boldsymbol {Z_{2}}}\sinh {(\gamma _{2}x)}\end{matrix}}\right]\left[{\begin{matrix}{\boldsymbol {I_{0r}}}\\{\boldsymbol {I_{1r}}}\\{\boldsymbol {I_{2r}}}\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8acdae43770b8f2308afda1254983d9262310a89)
![{\displaystyle \left[{\begin{matrix}{\boldsymbol {I_{0}}}(x)\\{\boldsymbol {I_{1}}}(x)\\{\boldsymbol {I_{2}}}(x)\end{matrix}}\right]=\left[{\begin{matrix}{\frac {1}{\boldsymbol {Z_{0}}}}\sinh {(\gamma _{0}x)}&&\\&{\frac {1}{\boldsymbol {Z_{1}}}}\sinh {(\gamma _{1}x)}&\\&&{\frac {1}{\boldsymbol {Z_{2}}}}\sinh {(\gamma _{2}x)}\end{matrix}}\right]\left[{\begin{matrix}{\boldsymbol {V_{0r}}}\\{\boldsymbol {V_{1r}}}\\{\boldsymbol {V_{2r}}}\end{matrix}}\right]+\left[{\begin{matrix}\cosh {(\gamma _{0}x)}&&\\&\cosh {(\gamma _{1}x)}&\\&&\cosh {(\gamma _{2}x)}\end{matrix}}\right]\left[{\begin{matrix}{\boldsymbol {I_{0r}}}\\{\boldsymbol {I_{1r}}}\\{\boldsymbol {I_{2r}}}\end{matrix}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce6aa3521ed9d631b95061b94b772b9988fd79a8)