AC Power Transmission

From Open Electrical
Jump to navigation Jump to search

Introduction

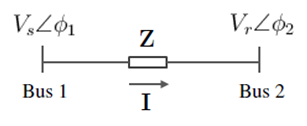
Consider the following model depicting the transfer of AC power between two buses across a line:

Figure 1. Simple AC power transmission model


Where is the voltage and phase angle at the sending end

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{V_{r}} = V_{r} e^{-j\phi_{2}} \, } is the voltage and phase angle at the receiving end
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{Z} \, } is the complex impedance of the line.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{I} = \frac{\boldsymbol{V_{s}} - \boldsymbol{V_{r}}}{\boldsymbol{Z}} \, } is the current phasor

The complex AC power transmitted to the receiving end bus can be calculated as follows:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{S} = \boldsymbol{V_{r}}\boldsymbol{I}^{*} }

At this stage, the impedance is purposely undefined and in the following sections, two different line impedance models will be introduced to illustrate the following fundamental features of AC power transmission:

  • The power-angle relationship
  • PV curves and steady-state voltage stability

Power-Angle Relationship

In its simplest form, we neglect the line resistance and capacitance and represent the line as purely inductive, i.e. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{Z} = j \omega L = jX \, } . The power transfer across the line is therefore:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{S} = \boldsymbol{V_{r}} \left[ \frac{\boldsymbol{V_{s}} - \boldsymbol{V_{r}}}{jX} \right]^{*} }
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{V_{r} e^{-j\phi_{2}}(V_{s} e^{j\phi_{1}} - V_{r} e^{j\phi_{2}})}{-jX} }
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = j \frac{V_{s} V_{r}}{X} e^{-j (\phi_{2} - \phi_{1})} - j \frac{V_{r}^{2}}{X}}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{V_{s} V_{r}}{X} \sin\delta + j \frac{V_{r}}{X} (V_{s} \cos\delta - V_{r}) }

Where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta = \phi_{2} - \phi_{1} \, } is called the power angle, which is the phase difference between the voltages on bus 1 and bus 2.

We can see that active and reactive power transfer can be characterised as follows:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P = \frac{V_{s} V_{r}}{X} \sin\delta }
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q = \frac{V_{r}}{X} (V_{s} \cos\delta - V_{r}) }

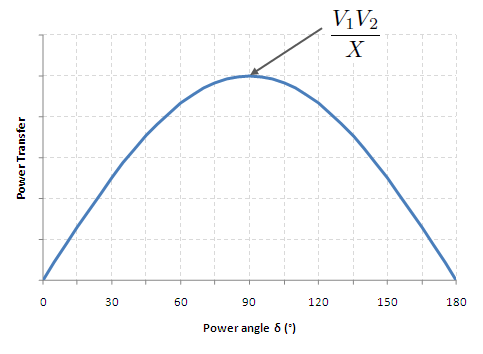
Plotting the active power transfer for various values of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta \, } , we get:

Figure 2. Active power transfer characteristic for a lossless line


The figure above is often used to articulate the Power-Angle Relationship. We can see that in this simple model, power will only flow when there is a phase difference between the voltages at the sending and receiving ends. Moreover, there is a theoretical limit to how much power can be transmitted through a line (shown here when the phase difference is 90o). This limit will be a recurring theme in these line models, i.e. lines have natural capacity limits on how much power they can transmit.

Steady-State Voltage Stability Limits

The lossless (L) line model can be made more realistic by adding a resistive component, i.e. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{Z} = R + jX = Z e^{j \theta} \, } . The power transfer across the line is therefore:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{S} = \boldsymbol{V_{r}}\left[ \frac{\boldsymbol{V_{s}} - \boldsymbol{V_{r}}}{R + jX} \right]^{*} }
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{V_{r} e^{-j\phi_{2}}(V_{s} e^{j\phi_{1}} - V_{r} e^{j\phi_{2}})}{Z e^{-j \theta}} }
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{V_{s} V_{r}}{Z} e^{-j (\phi_{2} - \phi_{1} - \theta)} - \frac{V_{r}^{2}}{Z} e^{j \theta}}

From the above equation, the active and reactive power transfer can be shown to be:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P = \frac{V_{s} V_{r}}{Z} \cos (\delta - \theta) - \frac{V_{r}^{2}}{Z} \cos \theta }
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q = - \frac{V_{s} V_{r}}{Z} \sin (\delta - \theta) - \frac{V_{r}^{2}}{Z} \sin \theta }

From the active power equation, we can solve for the voltage at bus 2 using the quadratic equation, i.e.:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{r} =\frac{-b \pm \sqrt {b^2-4ac}}{2a},}

Where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a = \frac{\cos \theta}{Z} \, }

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b = \frac{V_{s}}{Z} \cos (\delta - \theta) \, }
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c = -P \, }

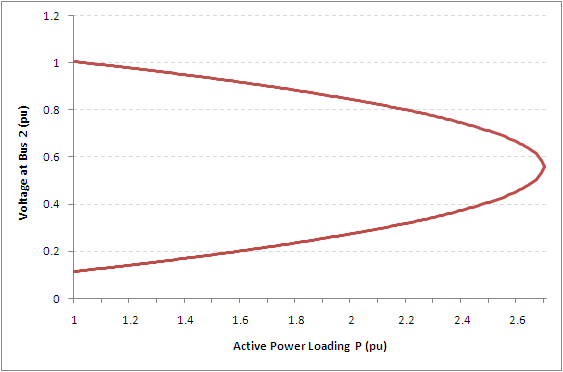
By keeping the voltage at bus 1, power angle and line impedance constant, we can plot the effect of increasing the active power on the voltage at bus 2 on a PV curve:

Figure 3. PV Curve at Bus 2 for a RL line


The PV curve shows that the voltage at bus 2 falls as the active power loading increases. The voltage falls until it hits a critical point (around 2.7pu loading) where the quadratic equation is no longer solvable. This is referred to as the "nose point" or "point of voltage collapse", and is the theoretical steady-state stability limit of the line.

Related Topics

Retrieved from "http://openelectrical.org/index.php?title=AC_Power_Transmission&oldid=24"