Photovoltaic Cell Model
The photovoltaic (PV) cell converts solar energy into electrical energy (direct current). It is often useful to take a cell operating at a certain solar irradiance and temperature and calculate its electrical output characteristics (i.e. voltage-current (V-I) curve). It is also desirable to perform these calculations using commonly available manufacturer data, e.g. open circuit voltage, short circuit current, voltage and current at maximum power point.
In this article, we will look at several models to approximate the V-I characteristics of a photovoltaic cell.
Solar Irradiance and Temperature Corrections
The parameters of a PV cell found in manufacturer data sheets are typically quoted at Standard Test Conditions (STC): an irradiance of 1,000 Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W/m^{2}} , the standard reference spectral irradiance with Air Mass 1.5 (see the NREL site for more details) and a cell temperature of 25 deg C.
When a PV cell is operating at different values of irradiance and temperature, the manufacturer parameters must first be corrected as follows:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{oc} = V_{oc, STC} \times \frac{\ln{E}}{\ln{1000}} \left[ 1 + \alpha (\theta - 25) \right] \,}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_{sc} = I_{sc, STC} \times \frac{E}{1000} \left[ 1 + \beta (\theta - 25) \right] \,}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{mpp} = V_{mpp, STC} \times \frac{\ln{E}}{\ln{1000}} \left[ 1 + \alpha (\theta - 25) \right] \,}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_{mpp} = I_{mpp, STC} \times \frac{E}{1000} \left[ 1 + \beta (\theta - 25) \right] \,}
Where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{oc} \, } is the cell open circuit voltage (Vdc)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_{sc} \, } is the cell short circuit current (A)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{mpp} \, } is the cell voltage at maximum power point (Vdc)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_{mpp} \, } is the cell current at maximum power point (A)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_{STC} \, } refers to the parameter X at standard test conditions, e.g. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{oc, STC} \, } is the open circuit voltage at STC
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E \, } is the actual operating irradiance (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W/m^{2}} )
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta \, } is the actual operating temperature (deg C)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha \, } is the temperature coefficient for voltage (pu)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta \, } is the temperature coefficient for current (pu)
Approximation of PV Cell V-I Characteristics
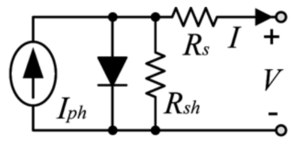
The single diode model (SDM) with the equivalent circuit as shown in the figure right is a simple model that is commonly used because of its practicality and the fact that it represents a reasonable compromise between accuracy and simplicity [1]. For a given voltage (V), the current from the cell (I) is approximated by the following well-known equation:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I = I_{ph} - I_{s} \left( \exp \left[ \frac{V + R_{s} I}{V_{T}} \right] - 1 \right) - \frac{V + R_{s}I}{R_{sh}} \,} (1)
Where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_{ph} \,} is the photon current
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_{s} \,} is the reverse saturation current
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{T} \,} is the thermal voltage
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{s} \,} is the series resistance
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{sh} \,} is the shunt resistance
Notice that this equation does not include the parameters commonly provided by a PV cell / module manufacturer (e.g. open circuit voltage, short circuit current, etc), which makes it limited in terms of practical value. A number of approaches have been proposed in the literature to convert this equation into a form such that a PV cell can be modelled (i.e. derive the V-I characteristics) using only the manufacturer data. The different approaches are typically approximations of the SDM with simplifying assumptions made to make the final equations somewhat tractable. In the subsections below, several of these approaches are presented.
ISDM Approximation
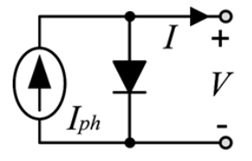
The ideal single diode model (ISDM) shown in the figure right is a simplification of the SDM, neglecting the influence of the series and shunt losses Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{s} \,} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{sh} \,} . The ISDM is the simplest model and is not highly accurate, particularly because the series resistance is neglected.
Key Assumptions of the ISDM Approximation:
- Shunt resistance Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{sh} \,} is infinite at operating points near MPP
- Series resistance Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{s} \,} is zero
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \exp \left[ \frac{V + R_{s} I}{V_{T}} \right] - 1 >> 1 } for all operating points
- The photon current is equal to the short circuit current, i.e. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_{ph} = I_{sc} \, }
If we apply these assumptions to Equation (1) above, we get the following reduced equation:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I = I_{sc} - I_{s} \exp \left[ \frac{V}{V_{T}} \right] \,} (2)
At open circuit, the current is equal to zero. Therefore:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_{sc} = I_{s} \exp \left[ \frac{V_{oc}}{V_{T}} \right] \,}
Re-arranging, we can solve for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_{s} \,} :
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_{s} = I_{sc} \exp \left[ -\frac{V_{oc}}{V_{T}} \right] \,}
Plugging the above equation into Equation (2), we get:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I = I_{sc} \left( 1 - \exp \left[ \frac{V - V_{oc}}{V_{T}} \right] \right) \,} (3)
At maximum power point (MPP), the cell voltage and current is known from the manufacturer data sheet as Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{mpp} \,} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_{mpp} \,} respectively. Putting these values into Equation (3):
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_{mpp} = I_{sc} \left( 1 - \exp \left[ \frac{V_{mpp} - V_{oc}}{V_{T}} \right] \right) \,}
Re-arranging, we can solve for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{T} \,} :
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{T} = \frac{V_{mpp} - V_{oc}}{\ln{\left( 1 - \frac{I_{mpp}}{I_{sc}} \right)}} \,} :
Finally, we get the V-I characteristic of the PV cell by plugging the above expression into Equation (3):
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I = I_{sc} \left( 1 - \exp \left[ \frac{\ln{\left( 1 - \frac{I_{mpp}}{I_{sc}} \right)} (V - V_{oc})}{V_{mpp} - V_{oc}} \right] \right) \,}
References
- [1] M.A de Blas, J.L Torres, E Prieto, A Garcıa, "Selecting a suitable model for characterizing photovoltaic devices”, Renewable Energy, vol. 25, pp. 371-380, March 2002.