Clarke Transform

From Open Electrical
Revision as of 07:51, 22 November 2020 by Jules (talk | contribs) (Created page with "The Clarke or <math>\alpha \beta 0 \,</math> transform is a space vector transformation of time-domain signals (e.g. voltage, current, flux, etc) from a natural three-phase co...")
(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)
Jump to navigation Jump to search

The Clarke or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha \beta 0 \,} transform is a space vector transformation of time-domain signals (e.g. voltage, current, flux, etc) from a natural three-phase coordinate system (ABC) into a stationary two-phase reference frame (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha \beta 0 \,} ). It is named after electrical engineer Edith Clarke [1].

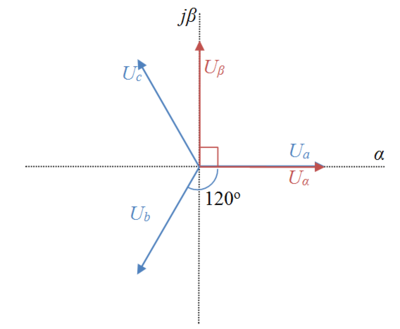
Three-phase and two-phase stationary reference frames

Consider the voltage phasors in the figure to the right. In the natural reference frame, the voltage distribution of the three stationary axes Ua, Ub, and Uc are 120o apart from each other. Cartesian axes are also portrayed, where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_{\alpha}} is the horizontal axis aligned with phase Ua, and the vertical axis rotated by 90o is indicated by Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle U_{\beta }} . Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_{\alpha}} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_{\beta}} have the same magnitude in per unit.

Three-phase voltages varying in time along the axes a, b, and c, can be algebraically transformed into two-phase voltages, varying in time along the axes Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta} by the following transformation matrix:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{\alpha \beta 0} = \frac{2}{3}\begin{bmatrix} 1 & -\frac{1}{2} & -\frac{1}{2} \\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ \end{bmatrix} }

The inverse transformation can also be obtained to transform the quantities back from two-phase to three-phase:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{\alpha \beta 0}^{-1} = \begin{bmatrix} 1 & 0 & 1\\ -\frac{1}{2} & \frac{\sqrt{3}}{2} & 1\\ -\frac{1}{2} & -\frac{\sqrt{3}}{2} & 1\end{bmatrix} }

It is interesting to note that the 0-component in the Clarke transform is the same as the zero sequence component in the symmetrical components transform. For example, for voltages Ua, Ub and Uc, the zero sequence component for both the Clarke and symmetrical components transforms is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3} \left( U_{a} + U_{b} + U_{c} \right) } .

Clarke Transform of Balanced Three-Phase Voltages

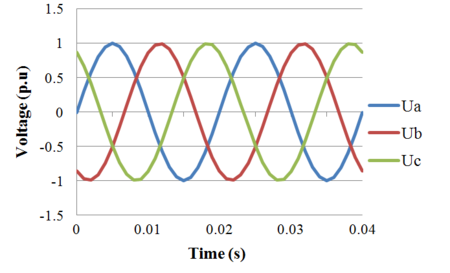
Consider the following balanced three-phase voltage waveforms:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{bmatrix} U_{a} \\ U_{b} \\ U_{c} \\ \end{bmatrix} = \begin{bmatrix} U_{m} \cos(\omega t) \\ U_{m} \cos(\omega t + \frac{2\pi}{3}) \\ U_{m} \cos(\omega t - \frac{2\pi}{3}) \\ \end{bmatrix} }

Taking the Clarke transform, we get:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{bmatrix} U_{\alpha} \\ U_{\beta} \\ U_{0} \\ \end{bmatrix} = T_{\alpha \beta 0} \begin{bmatrix} U_{a} \\ U_{b} \\ U_{c} \\ \end{bmatrix} }
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{2}{3}\begin{bmatrix} 1 & -\frac{1}{2} & -\frac{1}{2} \\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ \end{bmatrix} \begin{bmatrix} U_{m} \cos(\omega t) \\ U_{m} \cos(\omega t + \frac{2\pi}{3}) \\ U_{m} \cos(\omega t - \frac{2\pi}{3}) \\ \end{bmatrix} }
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \begin{bmatrix} \frac{2U_{m}}{3} \left[ \cos(\omega t) - \frac{1}{2} \cos(\omega t + \frac{2\pi}{3}) - \frac{1}{2} \cos(\omega t - \frac{2\pi}{3}) \right] \\ \frac{\sqrt{3} U_{m}}{3} \left[ \cos(\omega t + \frac{2\pi}{3}) - \cos(\omega t - \frac{2\pi}{3}) \right] \\ \frac{U_{m}}{3} \left[ \cos(\omega t) + \cos(\omega t + \frac{2\pi}{3}) + \cos(\omega t - \frac{2\pi}{3}) \right] \\ \end{bmatrix} }
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \begin{bmatrix} U_{m} \cos(\omega t) \\ U_{m} \sin(\omega t) \\ 0 \\ \end{bmatrix} }

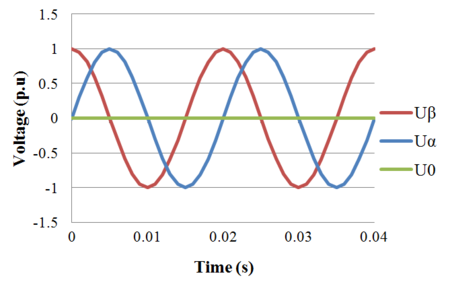
Time domain simulation result of transformation from three-phase stationary into two-phase stationary coordinated system is shown in the following figures:

Three-phase voltages in the time domain
Transformation of three-phase voltages into two-phase orthogonal voltages

From the equations and figures above, it can be concluded that in the balanced condition, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_{\alpha}} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_{\beta}} are sinusoidal functions and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_{0}} is zero.

Clarke Transform of Balanced Three-Phase Currents

Similarly, one can calculate the Clarke transform of balanced three-phase currents (which lags the voltage by an arbitrary angle Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta} ):

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{bmatrix} I_{a} \\ I_{b} \\ I_{c} \\ \end{bmatrix} = \begin{bmatrix} I_{m} \cos(\omega t - \delta) \\ I_{m} \cos(\omega t - \delta + \frac{2\pi}{3}) \\ I_{m} \cos(\omega t - \delta - \frac{2\pi}{3}) \\ \end{bmatrix} }

Using the same procedure as before, the Clarke transform is:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{bmatrix} I_{\alpha} \\ I_{\beta} \\ I_{0} \\ \end{bmatrix} = T_{\alpha \beta 0} \begin{bmatrix} I_{a} \\ I_{b} \\ I_{c} \\ \end{bmatrix} }
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \begin{bmatrix} I_{m} \cos(\omega t - \delta) \\ I_{m} \sin(\omega t - \delta) \\ 0 \\ \end{bmatrix} }

We can see that as in the voltage case, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_{\alpha}} is a cosine function, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_{\beta}} is a sine function and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U=I_{0}} is zero. However note the lagging phase angle Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta} .

Derivation of Transformation Matrix

As three phase voltages can be represented in 2D complex plane like vectors, the transformation can be done by using same idea. If vector decomposition is used, it can be seen that:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_{\alpha} = U_{a} \cos(0) - U_{b} \cos(\frac{\pi}{3}) - U_{c} \cos(\frac{\pi}{3}) }
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_{\beta} = U_{a} \cos(\frac{\pi}{2}) + U_{b} \cos(\frac{\pi}{6}) - U_{c} \cos(\frac{\pi}{6}) }

To obtain zero component, every phase voltage can be summed with equal weights to reveal any imbalances between phases or DC component. Therefore;

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_{0} = U_{a} k_{0} + U_{b} k_{0} + U_{c} k_{0} \,}

If these are written in matrix form;

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{bmatrix} U_{\alpha} \\ U_{\beta} \\ U_{0} \\ \end{bmatrix} =k_{1} \begin{bmatrix} 1 & -\frac{1}{2} & -\frac{1}{2} \\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \\ k_{0} & k_{0} & k_{0} \\ \end{bmatrix} \begin{bmatrix} U_{a} \\ U_{b} \\ U_{c} \\ \end{bmatrix} }

Here a different constant, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_{1}} , is added as a correction factor to remove scaling errors that occured due to multiplication. These constants are selected as Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_{1} = \frac{2}{3}} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_{0} = \frac{1}{2}} above as standard values. However, there are also another possibilities to select these coefficients. Another approach can be reduction of gain in matrix to 1 [2].

Let us calculate the gain caused by the matrix coefficients for the first row;

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G = \sqrt{{1}^{2} + {(-\frac{1}{2})}^{2} + {(-\frac{1}{2})}^{2} } = \sqrt{\frac{3}{2}} }

The same result can be obtained for second row if the necesssary calculations are done. To reduce this gain to unity value, a coefficent should be added as;

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_{1} = \frac{1}{G} = \sqrt{\frac{2}{3}} }

And value of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_{0} } can be calculated from by using;

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_{0} = \sqrt{3{k_{0}}^{2}} }
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_{0} = G \,}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{3{k_{0}}^{2}} = \sqrt{\frac{3}{2}} }
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_{0} = \frac{1}{\sqrt{2}} }

In matrix form:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{bmatrix} U_{\alpha} \\ U_{\beta} \\ U_{0} \\ \end{bmatrix} =\sqrt{\frac{2}{3}} \begin{bmatrix} 1 & -\frac{1}{2} & -\frac{1}{2} \\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \end{bmatrix} \begin{bmatrix} U_{a} \\ U_{b} \\ U_{c} \\ \end{bmatrix} }

Use of different approaches have different advantages and disadvantages. Advantage of this different selection of coefficients brings the power invariancy.

In first method power can be written as;

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S = {\begin{bmatrix} U_{a} \\ U_{b} \\ U_{c} \\ \end{bmatrix}}^T {\begin{bmatrix} I_{a} \\ I_{b} \\ I_{c} \\ \end{bmatrix}} = {(T_{\alpha \beta 0}^{-1} \begin{bmatrix} U_{\alpha} \\ U_{\beta} \\ U_{0} \\ \end{bmatrix})}^T {(T_{\alpha \beta 0}^{-1} \begin{bmatrix} I_{\alpha} \\ I_{\beta} \\ I_{0} \\ \end{bmatrix})} = {(\begin{bmatrix} U_{\alpha} \\ U_{\beta} \\ U_{0} \\ \end{bmatrix})}^T {(T_{\alpha \beta 0}^{-1})}^T (T_{\alpha \beta 0}^{-1}) {(\begin{bmatrix} I_{\alpha} \\ I_{\beta} \\ I_{0} \\ \end{bmatrix})} }

Here the multiplication of 2 transformation matrices can be found as following in the first approach;

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {(T_{\alpha \beta 0}^{-1})}^T (T_{\alpha \beta 0}^{-1}) = \begin{bmatrix} \frac{3}{2} & 0 & 0 \\ 0 & \frac{3}{2} & 0 \\ 0 & 0 & 3 \\ \end{bmatrix} }

which causes power to be:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S = U_{a}I_{a} + U_{b}I_{b} + U_{c}I_{c} = \frac{3}{2}(U_{\alpha}I_{\alpha} + U_{\beta}I_{\beta} + 2U_{0}I_{0}) }

However, in the second approach where the coefficients are reduced to unity;

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {(T_{\alpha \beta 0}^{-1})}^T (T_{\alpha \beta 0}^{-1}) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} }

and the power;

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S = U_{a}I_{a} + U_{b}I_{b} + U_{c}I_{c} = (U_{\alpha}I_{\alpha} + U_{\beta}I_{\beta} + U_{0}I_{0}) \, }

References

Related Topics

Retrieved from "http://openelectrical.org/index.php?title=Clarke_Transform&oldid=101"