The Clarke or  transform is a space vector transformation of time-domain signals (e.g. voltage, current, flux, etc) from a natural three-phase coordinate system (ABC) into a stationary two-phase reference frame (
transform is a space vector transformation of time-domain signals (e.g. voltage, current, flux, etc) from a natural three-phase coordinate system (ABC) into a stationary two-phase reference frame ( ). It is named after electrical engineer Edith Clarke [1].
). It is named after electrical engineer Edith Clarke [1].
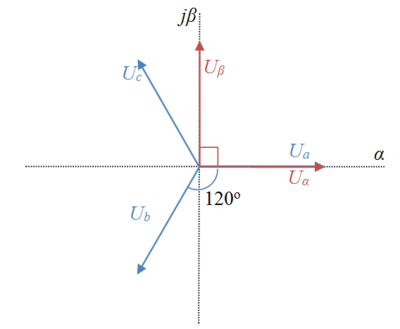
Three-phase and two-phase stationary reference frames
Consider the voltage phasors in the figure to the right. In the natural reference frame, the voltage distribution of the three stationary axes Ua, Ub, and Uc are 120o apart from each other. Cartesian axes are also portrayed, where  is the horizontal axis aligned with phase Ua, and the vertical axis rotated by 90o is indicated by
is the horizontal axis aligned with phase Ua, and the vertical axis rotated by 90o is indicated by  .
.  and
and  have the same magnitude in per unit.
have the same magnitude in per unit.
Three-phase voltages varying in time along the axes a, b, and c, can be algebraically transformed into two-phase voltages, varying in time along the axes  and
and  by the following transformation matrix:
by the following transformation matrix:

The inverse transformation can also be obtained to transform the quantities back from two-phase to three-phase:

It is interesting to note that the 0-component in the Clarke transform is the same as the zero sequence component in the symmetrical components transform. For example, for voltages Ua, Ub and Uc, the zero sequence component for both the Clarke and symmetrical components transforms is  .
.
Clarke Transform of Balanced Three-Phase Voltages
Consider the following balanced three-phase voltage waveforms:

Taking the Clarke transform, we get:


![{\displaystyle ={\begin{bmatrix}{\frac {2U_{m}}{3}}\left[\cos(\omega t)-{\frac {1}{2}}\cos(\omega t+{\frac {2\pi }{3}})-{\frac {1}{2}}\cos(\omega t-{\frac {2\pi }{3}})\right]\\{\frac {{\sqrt {3}}U_{m}}{3}}\left[\cos(\omega t+{\frac {2\pi }{3}})-\cos(\omega t-{\frac {2\pi }{3}})\right]\\{\frac {U_{m}}{3}}\left[\cos(\omega t)+\cos(\omega t+{\frac {2\pi }{3}})+\cos(\omega t-{\frac {2\pi }{3}})\right]\\\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2e04e1fa7c079276abad8ad19362b5cea650938)

Time domain simulation result of transformation from three-phase stationary into two-phase stationary coordinated system is shown in the following figures:
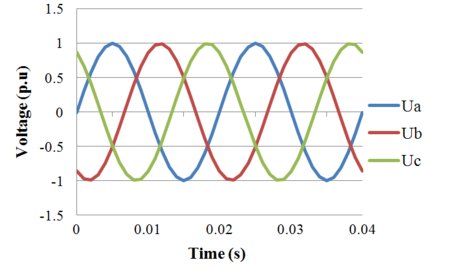
Three-phase voltages in the time domain
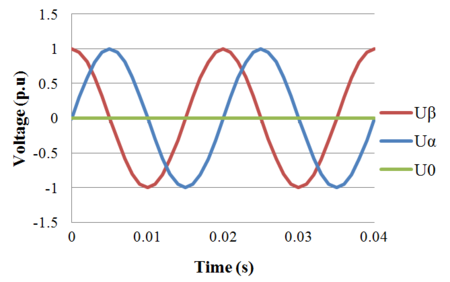
Transformation of three-phase voltages into two-phase orthogonal voltages
From the equations and figures above, it can be concluded that in the balanced condition,  and
and  are sinusoidal functions and
are sinusoidal functions and  is zero.
is zero.
Clarke Transform of Balanced Three-Phase Currents
Similarly, one can calculate the Clarke transform of balanced three-phase currents (which lags the voltage by an arbitrary angle  ):
):

Using the same procedure as before, the Clarke transform is:


We can see that as in the voltage case,  is a cosine function,
is a cosine function,  is a sine function and
is a sine function and  is zero. However note the lagging phase angle
is zero. However note the lagging phase angle  .
.
Derivation of Transformation Matrix
As three phase voltages can be represented in 2D complex plane like vectors, the transformation can be done by using same idea. If vector decomposition is used, it can be seen that:


To obtain zero component, every phase voltage can be summed with equal weights to reveal any imbalances between phases or DC component. Therefore;

If these are written in matrix form;

Here a different constant,  , is added as a correction factor to remove scaling errors that occured due to multiplication. These constants are selected as
, is added as a correction factor to remove scaling errors that occured due to multiplication. These constants are selected as  and
and  above as standard values. However, there are also another possibilities to select these coefficients. Another approach can be reduction of gain in matrix to 1 [2].
above as standard values. However, there are also another possibilities to select these coefficients. Another approach can be reduction of gain in matrix to 1 [2].
Let us calculate the gain caused by the matrix coefficients for the first row;

The same result can be obtained for second row if the necesssary calculations are done. To reduce this gain to unity value, a coefficent should be added as;

And value of  can be calculated from by using;
can be calculated from by using;




In matrix form:

Use of different approaches have different advantages and disadvantages. Advantage of this different selection of coefficients brings the power invariancy.
In first method power can be written as;

Here the multiplication of 2 transformation matrices can be found as following in the first approach;

which causes power to be:

However, in the second approach where the coefficients are reduced to unity;

and the power;

References
Related Topics












![{\displaystyle ={\begin{bmatrix}{\frac {2U_{m}}{3}}\left[\cos(\omega t)-{\frac {1}{2}}\cos(\omega t+{\frac {2\pi }{3}})-{\frac {1}{2}}\cos(\omega t-{\frac {2\pi }{3}})\right]\\{\frac {{\sqrt {3}}U_{m}}{3}}\left[\cos(\omega t+{\frac {2\pi }{3}})-\cos(\omega t-{\frac {2\pi }{3}})\right]\\{\frac {U_{m}}{3}}\left[\cos(\omega t)+\cos(\omega t+{\frac {2\pi }{3}})+\cos(\omega t-{\frac {2\pi }{3}})\right]\\\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2e04e1fa7c079276abad8ad19362b5cea650938)






























