The dq0 transform (often called the Park transform) is a space vector transformation of three-phase time-domain signals from a stationary phase coordinate system (ABC) to a rotating coordinate system (dq0).
The transform applied to time-domain voltages in the natural frame (i.e.  ,
,  and
and  ) is as follows:
) is as follows:

Where  is the angle between the rotating and fixed coordinate system at each time t and
is the angle between the rotating and fixed coordinate system at each time t and  is an initial phase shift of the voltage.
is an initial phase shift of the voltage.
The inverse transformation from the dq0 frame to the natural abc frame:

As in the Clarke Transform, it is interesting to note that the 0-component above is the same as the zero sequence component in the symmetrical components transform. For example, for voltages Ua, Ub and Uc, the zero sequence component for both the dq0 and symmetrical components transforms is  .
.
The remainder of this article provides some of the intuition behind why the dq0 transform is so useful in electrical engineering.
Background
The dq0 transform is essentially an extension of the Clake transform, applying an angle transformation to convert from a stationary reference frame to a synchronously rotating frame. The synchronous reference frame can be aligned to rotate with the voltage (e.g. used in voltage source converters) or with the current (e.g. used in current source converters).
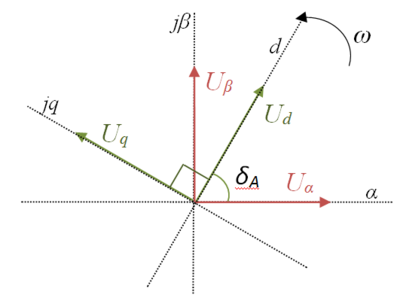
Historically however, the dq0 transform was introduced earlier than the Clarke transform by R. H. Park in his seminal 1929 paper on synchronous machine modelling [1].
Classical dq0 Transform in Balanced Systems
dq0 Transform of Balanced Three-Phase Voltages
The following equations take a two-phase quadrature voltage along the stationary frame and transforms it into a two-phase synchronous frame (with a reference frame aligned to the voltage):

Note that in the dq0 frame, the 0-component is the same as that in the  frame. Moreover, as we saw in the Clarke transform, the 0-component is zero for balanced three-phase systems. Therefore in the following discussion on balanced systems, the 0-component will be omitted.
frame. Moreover, as we saw in the Clarke transform, the 0-component is zero for balanced three-phase systems. Therefore in the following discussion on balanced systems, the 0-component will be omitted.
Consider a balanced three-phase voltage with  components as follows:
components as follows:

The dq0 transform of this voltage is:

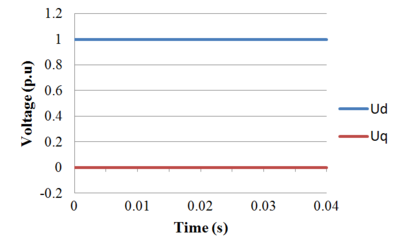
Suppose that we are using a voltage reference frame and will align the synchronous frame with the voltage. Therefore  and:
and:


It can be observed that since the synchronous frame is aligned to rotate with the voltage, the d-component corresponds to the magnitude of the voltage and the q-component is zero. A plot of the transformation of a voltage from a stationary  frame into rotating dq frame is shown in the figure below.
frame into rotating dq frame is shown in the figure below.
The inverse transform is as follows:

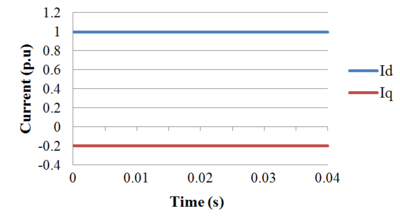
dq0 Transform of Balanced Three-Phase Currents
The dq0 transformation can be similarly applied to the current. From a two-phase quadrature stationary ( ) current of the form (where
) current of the form (where  is the angle at which the current lags the voltage):
is the angle at which the current lags the voltage):

We transform it into a two-phase synchronous (dq0) frame:



Instantaneous Power in dq0 Frame
The instantaneous active and reactive power from a set of two-phase (dq) voltages and currents are:


When the synchronous frame is aligned to voltage, we saw earlier that the quadrature component :  . Therefore, the power equations reduce to:
. Therefore, the power equations reduce to:


The above equations show that independent control of active and reactive power is possible by means of controlling the dq current components ( and
and  ).
).
Summary of dq0 Transform in Balanced Systems
For three-phase balanced systems, the dq0 transform has the following advantageous characteristics:
- 1) The dq0 transform reduces three-phase AC quantities (e.g.
 ,
,  and
and  ) into two DC quantities (e.g.
) into two DC quantities (e.g.  ,
,  ). For balanced systems, the 0-component is zero. The DC quantities facilitate easier filtering and control.
). For balanced systems, the 0-component is zero. The DC quantities facilitate easier filtering and control.
- 2) Active and reactive power can be controlled independently by controlling the dq components.
Power Invariant Formulation
The classical Park transform is not power invariant, i.e. the instantaneous power of the variables calculated in the dq0 frame is not the same as the power calculated in the natural coordinate reference frame. A power invariant version of the dq0 transform is as follows:

Inverse transform:

References
Related Topics




































